On this article, you’ll be taught three expert-level characteristic engineering methods — counterfactual options, domain-constrained representations, and causal-invariant options — for constructing sturdy and explainable fashions in high-stakes settings.
Matters we’ll cowl embrace:
- The way to generate counterfactual sensitivity options for decision-boundary consciousness.
- The way to practice a constrained autoencoder that encodes a monotonic area rule into its illustration.
- The way to uncover causal-invariant options that stay steady throughout environments.
With out additional delay, let’s start.

Skilled-Degree Characteristic Engineering: Superior Strategies for Excessive-Stakes Fashions
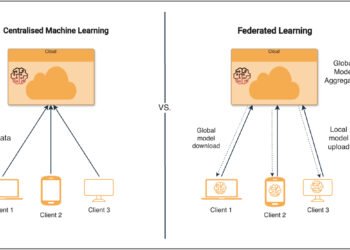
Picture by Editor
Introduction
Constructing machine studying fashions in high-stakes contexts like finance, healthcare, and significant infrastructure usually calls for robustness, explainability, and different domain-specific constraints. In these conditions, it may be price going past traditional characteristic engineering methods and adopting superior, expert-level methods tailor-made to such settings.
This text presents three such methods, explains how they work, and highlights their sensible impression.
Counterfactual Characteristic Technology
Counterfactual characteristic era contains methods that quantify how delicate predictions are to determination boundaries by developing hypothetical knowledge factors from minimal adjustments to unique options. The thought is straightforward: ask “how a lot should an unique characteristic worth change for the mannequin’s prediction to cross a vital threshold?” These derived options enhance interpretability — e.g. “how shut is a affected person to a analysis?” or “what’s the minimal revenue improve required for mortgage approval?”— they usually encode sensitivity immediately in characteristic house, which might enhance robustness.
The Python instance under creates a counterfactual sensitivity characteristic, cf_delta_feat0, measuring how a lot enter characteristic feat_0 should change (holding all others mounted) to cross the classifier’s determination boundary. We’ll use NumPy, pandas, and scikit-learn.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from sklearn.datasets import make_classification from sklearn.preprocessing import StandardScaler
# Toy knowledge and baseline linear classifier X, y = make_classification(n_samples=500, n_features=5, random_state=42) df = pd.DataFrame(X, columns=[f“feat_{i}” for i in range(X.shape[1])]) df[‘target’] = y
scaler = StandardScaler() X_scaled = scaler.fit_transform(df.drop(columns=“goal”)) clf = LogisticRegression().match(X_scaled, y)
# Determination boundary parameters weights = clf.coef_[0] bias = clf.intercept_[0]
def counterfactual_delta_feat0(x, eps=1e–9): “”“ Minimal change to characteristic 0, holding different options mounted, required to maneuver the linear logit rating to the choice boundary (0). For a linear mannequin: delta = -score / w0 ““” rating = np.dot(weights, x) + bias w0 = weights[0] return –rating / (w0 + eps)
df[‘cf_delta_feat0’] = [counterfactual_delta_feat0(x) for x in X_scaled] df.head() |
Area-Constrained Illustration Studying (Constrained Autoencoders)
Autoencoders are broadly used for unsupervised illustration studying. We will adapt them for domain-constrained illustration studying: be taught a compressed illustration (latent options) whereas imposing express area guidelines (e.g., security margins or monotonicity legal guidelines). Not like unconstrained latent components, domain-constrained representations are skilled to respect bodily, moral, or regulatory constraints.
Beneath, we practice an autoencoder that learns three latent options and reconstructs inputs whereas softly imposing a monotonic rule: increased values of feat_0 mustn’t lower the probability of the constructive label. We add a easy supervised predictor head and penalize violations by way of a finite-difference monotonicity loss. Implementation makes use of PyTorch.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
import torch import torch.nn as nn import torch.optim as optim from sklearn.model_selection import train_test_break up
# Supervised break up utilizing the sooner DataFrame `df` X_train, X_val, y_train, y_val = train_test_split( df.drop(columns=“goal”).values, df[‘target’].values, test_size=0.2, random_state=42 )
X_train = torch.tensor(X_train, dtype=torch.float32) y_train = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
torch.manual_seed(42)
class ConstrainedAutoencoder(nn.Module): def __init__(self, input_dim, latent_dim=3): tremendous().__init__() self.encoder = nn.Sequential( nn.Linear(input_dim, 8), nn.ReLU(), nn.Linear(8, latent_dim) ) self.decoder = nn.Sequential( nn.Linear(latent_dim, 8), nn.ReLU(), nn.Linear(8, input_dim) ) # Small predictor head on high of the latent code (logit output) self.predictor = nn.Linear(latent_dim, 1)
def ahead(self, x): z = self.encoder(x) recon = self.decoder(z) logit = self.predictor(z) return recon, z, logit
mannequin = ConstrainedAutoencoder(input_dim=X_train.form[1]) optimizer = optim.Adam(mannequin.parameters(), lr=1e–3) recon_loss_fn = nn.MSELoss() pred_loss_fn = nn.BCEWithLogitsLoss()
epsilon = 1e–2 # finite-difference step for monotonicity on feat_0 for epoch in vary(50): mannequin.practice() optimizer.zero_grad()
recon, z, logit = mannequin(X_train) # Reconstruction + supervised prediction loss loss_recon = recon_loss_fn(recon, X_train) loss_pred = pred_loss_fn(logit, y_train)
# Monotonicity penalty: y_logit(x + e*e0) – y_logit(x) must be >= 0 X_plus = X_train.clone() X_plus[:, 0] = X_plus[:, 0] + epsilon _, _, logit_plus = mannequin(X_plus)
mono_violation = torch.relu(logit – logit_plus) # unfavourable slope if > 0 loss_mono = mono_violation.imply()
loss = loss_recon + 0.5 * loss_pred + 0.1 * loss_mono loss.backward() optimizer.step()
# Latent options now mirror the monotonic constraint with torch.no_grad(): _, latent_feats, _ = mannequin(X_train) latent_feats[:5] |
Causal-Invariant Options
Causal-invariant options are variables whose relationship to the end result stays steady throughout totally different contexts or environments. By focusing on causal alerts quite than spurious correlations, fashions generalize higher to out-of-distribution settings. One sensible route is to penalize adjustments in danger gradients throughout environments so the mannequin can’t lean on environment-specific shortcuts.
The instance under simulates two environments. Solely the primary characteristic is really causal; the second turns into spuriously correlated with the label in surroundings 1. We practice a shared linear mannequin throughout environments whereas penalizing gradient mismatch, encouraging reliance on invariant (causal) construction.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import numpy as np import torch import torch.nn as nn import torch.optim as optim
torch.manual_seed(42) np.random.seed(42)
# Two environments with a spurious sign in env1 n = 300 X_env1 = np.random.randn(n, 2) X_env2 = np.random.randn(n, 2)
# True causal relation: y relies upon solely on X[:,0] y_env1 = (X_env1[:, 0] + 0.1*np.random.randn(n) > 0).astype(int) y_env2 = (X_env2[:, 0] + 0.1*np.random.randn(n) > 0).astype(int)
# Inject spurious correlation in env1 by way of characteristic 1 X_env1[:, 1] = y_env1 + 0.1*np.random.randn(n)
X1, y1 = torch.tensor(X_env1, dtype=torch.float32), torch.tensor(y_env1, dtype=torch.float32) X2, y2 = torch.tensor(X_env2, dtype=torch.float32), torch.tensor(y_env2, dtype=torch.float32)
class LinearModel(nn.Module): def __init__(self): tremendous().__init__() self.w = nn.Parameter(torch.randn(2, 1))
def ahead(self, x): return x @ self.w
mannequin = LinearModel() optimizer = optim.Adam(mannequin.parameters(), lr=1e–2)
def env_risk(x, y, w): logits = x @ w return torch.imply((logits.squeeze() – y)**2)
for epoch in vary(2000): optimizer.zero_grad() risk1 = env_risk(X1, y1, mannequin.w) risk2 = env_risk(X2, y2, mannequin.w)
# Invariance penalty: align danger gradients throughout environments grad1 = torch.autograd.grad(risk1, mannequin.w, create_graph=True)[0] grad2 = torch.autograd.grad(risk2, mannequin.w, create_graph=True)[0] penalty = torch.sum((grad1 – grad2)**2)
loss = (risk1 + risk2) + 100.0 * penalty loss.backward() optimizer.step()
print(“Realized weights:”, mannequin.w.knowledge.numpy().ravel()) |
Closing Remarks
We lined three superior characteristic engineering methods for high-stakes machine studying: counterfactual sensitivity options for decision-boundary consciousness, domain-constrained autoencoders that encode knowledgeable guidelines, and causal-invariant options that promote steady generalization. Used judiciously, these instruments could make fashions extra sturdy, interpretable, and dependable the place it issues most.
On this article, you’ll be taught three expert-level characteristic engineering methods — counterfactual options, domain-constrained representations, and causal-invariant options — for constructing sturdy and explainable fashions in high-stakes settings.
Matters we’ll cowl embrace:
- The way to generate counterfactual sensitivity options for decision-boundary consciousness.
- The way to practice a constrained autoencoder that encodes a monotonic area rule into its illustration.
- The way to uncover causal-invariant options that stay steady throughout environments.
With out additional delay, let’s start.

Skilled-Degree Characteristic Engineering: Superior Strategies for Excessive-Stakes Fashions
Picture by Editor
Introduction
Constructing machine studying fashions in high-stakes contexts like finance, healthcare, and significant infrastructure usually calls for robustness, explainability, and different domain-specific constraints. In these conditions, it may be price going past traditional characteristic engineering methods and adopting superior, expert-level methods tailor-made to such settings.
This text presents three such methods, explains how they work, and highlights their sensible impression.
Counterfactual Characteristic Technology
Counterfactual characteristic era contains methods that quantify how delicate predictions are to determination boundaries by developing hypothetical knowledge factors from minimal adjustments to unique options. The thought is straightforward: ask “how a lot should an unique characteristic worth change for the mannequin’s prediction to cross a vital threshold?” These derived options enhance interpretability — e.g. “how shut is a affected person to a analysis?” or “what’s the minimal revenue improve required for mortgage approval?”— they usually encode sensitivity immediately in characteristic house, which might enhance robustness.
The Python instance under creates a counterfactual sensitivity characteristic, cf_delta_feat0, measuring how a lot enter characteristic feat_0 should change (holding all others mounted) to cross the classifier’s determination boundary. We’ll use NumPy, pandas, and scikit-learn.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from sklearn.datasets import make_classification from sklearn.preprocessing import StandardScaler
# Toy knowledge and baseline linear classifier X, y = make_classification(n_samples=500, n_features=5, random_state=42) df = pd.DataFrame(X, columns=[f“feat_{i}” for i in range(X.shape[1])]) df[‘target’] = y
scaler = StandardScaler() X_scaled = scaler.fit_transform(df.drop(columns=“goal”)) clf = LogisticRegression().match(X_scaled, y)
# Determination boundary parameters weights = clf.coef_[0] bias = clf.intercept_[0]
def counterfactual_delta_feat0(x, eps=1e–9): “”“ Minimal change to characteristic 0, holding different options mounted, required to maneuver the linear logit rating to the choice boundary (0). For a linear mannequin: delta = -score / w0 ““” rating = np.dot(weights, x) + bias w0 = weights[0] return –rating / (w0 + eps)
df[‘cf_delta_feat0’] = [counterfactual_delta_feat0(x) for x in X_scaled] df.head() |
Area-Constrained Illustration Studying (Constrained Autoencoders)
Autoencoders are broadly used for unsupervised illustration studying. We will adapt them for domain-constrained illustration studying: be taught a compressed illustration (latent options) whereas imposing express area guidelines (e.g., security margins or monotonicity legal guidelines). Not like unconstrained latent components, domain-constrained representations are skilled to respect bodily, moral, or regulatory constraints.
Beneath, we practice an autoencoder that learns three latent options and reconstructs inputs whereas softly imposing a monotonic rule: increased values of feat_0 mustn’t lower the probability of the constructive label. We add a easy supervised predictor head and penalize violations by way of a finite-difference monotonicity loss. Implementation makes use of PyTorch.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
import torch import torch.nn as nn import torch.optim as optim from sklearn.model_selection import train_test_break up
# Supervised break up utilizing the sooner DataFrame `df` X_train, X_val, y_train, y_val = train_test_split( df.drop(columns=“goal”).values, df[‘target’].values, test_size=0.2, random_state=42 )
X_train = torch.tensor(X_train, dtype=torch.float32) y_train = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
torch.manual_seed(42)
class ConstrainedAutoencoder(nn.Module): def __init__(self, input_dim, latent_dim=3): tremendous().__init__() self.encoder = nn.Sequential( nn.Linear(input_dim, 8), nn.ReLU(), nn.Linear(8, latent_dim) ) self.decoder = nn.Sequential( nn.Linear(latent_dim, 8), nn.ReLU(), nn.Linear(8, input_dim) ) # Small predictor head on high of the latent code (logit output) self.predictor = nn.Linear(latent_dim, 1)
def ahead(self, x): z = self.encoder(x) recon = self.decoder(z) logit = self.predictor(z) return recon, z, logit
mannequin = ConstrainedAutoencoder(input_dim=X_train.form[1]) optimizer = optim.Adam(mannequin.parameters(), lr=1e–3) recon_loss_fn = nn.MSELoss() pred_loss_fn = nn.BCEWithLogitsLoss()
epsilon = 1e–2 # finite-difference step for monotonicity on feat_0 for epoch in vary(50): mannequin.practice() optimizer.zero_grad()
recon, z, logit = mannequin(X_train) # Reconstruction + supervised prediction loss loss_recon = recon_loss_fn(recon, X_train) loss_pred = pred_loss_fn(logit, y_train)
# Monotonicity penalty: y_logit(x + e*e0) – y_logit(x) must be >= 0 X_plus = X_train.clone() X_plus[:, 0] = X_plus[:, 0] + epsilon _, _, logit_plus = mannequin(X_plus)
mono_violation = torch.relu(logit – logit_plus) # unfavourable slope if > 0 loss_mono = mono_violation.imply()
loss = loss_recon + 0.5 * loss_pred + 0.1 * loss_mono loss.backward() optimizer.step()
# Latent options now mirror the monotonic constraint with torch.no_grad(): _, latent_feats, _ = mannequin(X_train) latent_feats[:5] |
Causal-Invariant Options
Causal-invariant options are variables whose relationship to the end result stays steady throughout totally different contexts or environments. By focusing on causal alerts quite than spurious correlations, fashions generalize higher to out-of-distribution settings. One sensible route is to penalize adjustments in danger gradients throughout environments so the mannequin can’t lean on environment-specific shortcuts.
The instance under simulates two environments. Solely the primary characteristic is really causal; the second turns into spuriously correlated with the label in surroundings 1. We practice a shared linear mannequin throughout environments whereas penalizing gradient mismatch, encouraging reliance on invariant (causal) construction.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import numpy as np import torch import torch.nn as nn import torch.optim as optim
torch.manual_seed(42) np.random.seed(42)
# Two environments with a spurious sign in env1 n = 300 X_env1 = np.random.randn(n, 2) X_env2 = np.random.randn(n, 2)
# True causal relation: y relies upon solely on X[:,0] y_env1 = (X_env1[:, 0] + 0.1*np.random.randn(n) > 0).astype(int) y_env2 = (X_env2[:, 0] + 0.1*np.random.randn(n) > 0).astype(int)
# Inject spurious correlation in env1 by way of characteristic 1 X_env1[:, 1] = y_env1 + 0.1*np.random.randn(n)
X1, y1 = torch.tensor(X_env1, dtype=torch.float32), torch.tensor(y_env1, dtype=torch.float32) X2, y2 = torch.tensor(X_env2, dtype=torch.float32), torch.tensor(y_env2, dtype=torch.float32)
class LinearModel(nn.Module): def __init__(self): tremendous().__init__() self.w = nn.Parameter(torch.randn(2, 1))
def ahead(self, x): return x @ self.w
mannequin = LinearModel() optimizer = optim.Adam(mannequin.parameters(), lr=1e–2)
def env_risk(x, y, w): logits = x @ w return torch.imply((logits.squeeze() – y)**2)
for epoch in vary(2000): optimizer.zero_grad() risk1 = env_risk(X1, y1, mannequin.w) risk2 = env_risk(X2, y2, mannequin.w)
# Invariance penalty: align danger gradients throughout environments grad1 = torch.autograd.grad(risk1, mannequin.w, create_graph=True)[0] grad2 = torch.autograd.grad(risk2, mannequin.w, create_graph=True)[0] penalty = torch.sum((grad1 – grad2)**2)
loss = (risk1 + risk2) + 100.0 * penalty loss.backward() optimizer.step()
print(“Realized weights:”, mannequin.w.knowledge.numpy().ravel()) |
Closing Remarks
We lined three superior characteristic engineering methods for high-stakes machine studying: counterfactual sensitivity options for decision-boundary consciousness, domain-constrained autoencoders that encode knowledgeable guidelines, and causal-invariant options that promote steady generalization. Used judiciously, these instruments could make fashions extra sturdy, interpretable, and dependable the place it issues most.