Rotary Place Embeddings (RoPE) is a method for encoding token positions in a sequence. It’s extensively utilized in many fashions and works properly for normal context lengths. Nevertheless, it requires adaptation for longer contexts. On this article, you’ll find out how RoPE is tailored for lengthy context size.
Let’s get began.

Rotary Place Embeddings for Lengthy Context Size
Picture by Nastya Dulhiier. Some rights reserved.
Overview
This text is split into two elements; they’re:
- Easy RoPE
- RoPE for Lengthy Context Size
Easy RoPE
In comparison with the sinusoidal place embeddings within the unique Transformer paper, RoPE mutates the enter tensor utilizing a rotation matrix:
$$
start{aligned}
X_{n,i} &= X_{n,i} cos(ntheta_i) – X_{n,frac{d}{2}+i} sin(ntheta_i)
X_{n,frac{d}{2}+i} &= X_{n,i} sin(ntheta_i) + X_{n,frac{d}{2}+i} cos(ntheta_i)
finish{aligned}
$$
the place $X_{n,i}$ is the $i$-th aspect of the vector on the $n$-th place of the sequence of tensor $X$. The size of every vector (also referred to as the hidden dimension or the mannequin dimension) is $d$. The amount $theta_i$ is the frequency of the $i$-th aspect of the vector. It’s computed as:
$$
theta_i = frac{1}{N^{2i/d}}
$$
A easy implementation of RoPE seems to be like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import torch import torch.nn as nn
def rotate_half(x: torch.Tensor) -> torch.Tensor: “”“Rotates half the hidden dims of the enter.
It is a helper operate for rotary place embeddings (RoPE). For a tensor of form (…, d), it returns a tensor the place the final d/2 dimensions are rotated by swapping and negating.
Args: x: Enter tensor of form (…, d)
Returns: Tensor of similar form with rotated final dimension ““” x1, x2 = x.chunk(2, dim=–1) return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation
class RotaryPositionEncoding(nn.Module): “”“Rotary place encoding.”“”
def __init__(self, dim: int, max_position_embeddings: int) -> None: “”“Initialize the RotaryPositionEncoding module
Args: dim: The hidden dimension of the enter tensor to which RoPE is utilized max_position_embeddings: The utmost sequence size of the enter tensor ““” tremendous().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) place = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(place, inv_freq) # save cosine and sine matrices as buffers self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin())
def ahead(self, x: torch.Tensor) -> torch.Tensor: “”“Apply RoPE to tensor x
Args: x: Enter tensor of form (batch_size, seq_length, num_heads, head_dim)
Returns: Output tensor of form (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.form dtype = x.dtype # remodel the cosine and sine matrices to 4D tensor and the identical dtype as x cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x output = (x * cos) + (rotate_half(x) * sin) return output |
The code above defines a tensor inv_freq because the inverse frequency of the RoPE, comparable to the frequency time period $theta_i$ within the formulation. It’s referred to as inverse frequency within the RoPE literature as a result of it’s inversely proportional to the wavelength (i.e., the utmost distance) that RoPE can seize.
Once you multiply two vectors from positions $p$ and $q$, as you’ll do within the scaled-dot product consideration, you discover that the outcome relies on the relative place $p – q$ because of the trigonometric identities:
$$
start{aligned}
cos(a – b) = cos(a) cos(b) + sin(a) sin(b)
sin(a – b) = sin(a) cos(b) – cos(a) sin(b)
finish{aligned}
$$
In language fashions, relative place sometimes issues greater than absolute place. Due to this fact, RoPE is usually a more sensible choice than the unique sinusoidal place embeddings.
RoPE for Lengthy Context Size
The capabilities $sin kx$ and $cos kx$ are periodic with interval $2pi/okay$. In RoPE, the time period $theta_i$ is known as the frequency time period as a result of it determines the periodicity. In a language mannequin, the high-frequency phrases are vital as a result of they assist perceive close by phrases in a sentence. The low-frequency phrases, nevertheless, are helpful for understanding context that spans throughout a number of sentences.
Due to this fact, while you design a mannequin with an extended context size, you need it to carry out properly for brief sentences since they’re extra widespread, however you additionally need it to deal with lengthy contexts that your mannequin ought to assist. You do not need RoPE to deal with each sequence size equally.
The technique is to reallocate the RoPE scaling funds: apply a scaling issue to enhance long-range stability (at low frequencies of sine and cosine) whereas avoiding scaling when native place info is vital (at excessive frequencies of sine and cosine).
In Llama variations 1 and a pair of, RoPE is carried out with a most size of 4096, just like the earlier part. In Llama 3.1, the mannequin’s context size is expanded to 131K tokens, however RoPE is calculated utilizing a base size of 8192. The implementation is as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
import torch import torch.nn as nn import math
def rotate_half(x: Tensor) -> Tensor: “”“Rotates half the hidden dims of the enter.
It is a helper operate for rotary place embeddings (RoPE). For a tensor of form (…, d), it returns a tensor the place the final d/2 dimensions are rotated by swapping and negating.
Args: x: Enter tensor of form (…, d)
Returns: Tensor of similar form with rotated final dimension ““” x1, x2 = x.chunk(2, dim=–1) return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation
class RotaryPositionEncoding(nn.Module): “”“Rotary place encoding.”“”
def __init__(self, dim: int, max_position_embeddings: int, base_length: int = 8192) -> None: “”“Initialize the RotaryPositionEncoding module
Args: dim: The hidden dimension of the enter tensor to which RoPE is utilized max_position_embeddings: The utmost sequence size of the enter tensor base_length: The bottom size of the RoPE ““” tremendous().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 scale_factor = 8.0 low_factor, high_factor = 1.0, 4.0 base_length = 8192 # Compute the inverse frequency based mostly on the usual RoPE formulation inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float().to(“cuda”) / dim)) # Compute the modified inverse frequency # scaled if freq too low, orig if freq too excessive, smoothed if in between wavelen = 2 * math.pi / inv_freq max_wavelen = base_length / low_factor min_wavelen = base_length / high_factor smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor) smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq inv_freq = torch.the place(wavelen > max_wavelen, inv_freq / scale_factor, torch.the place(wavelen < min_wavelen, inv_freq, smoothed)) # multiply with sequence size inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) place = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(place, inv_freq) # save cosine and sine matrices as buffers self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin())
def ahead(self, x: Tensor) -> Tensor: “”“Apply RoPE to tensor x
Args: x: Enter tensor of form (batch_size, seq_length, num_heads, head_dim)
Returns: Output tensor of form (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.form dtype = x.dtype # remodel the cosine and sine matrices to 4D tensor and the identical dtype as x cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x output = (x * cos) + (rotate_half(x) * sin) return output |
The constructor of the RotaryPositionEncoding class makes use of a extra subtle algorithm to compute the inv_freq tensor. The thought is to compute a wavelength for every frequency part, which represents the utmost distance between two tokens that the actual RoPE part can seize. If the wavelength is just too quick (or the frequency is just too excessive), the frequency stays unchanged. Nevertheless, if the wavelength is just too lengthy, the frequency is scaled down by the scale_factor, successfully lengthening the utmost distance that RoPE part can seize. To make sure stability, frequency parts between the high and low frequency thresholds are easily interpolated.
As an example the impact of scaling, you’ll be able to plot the ensuing inverse frequency with Matplotlib:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import matplotlib.pyplot as plt import torch import math
N = 10_000.0 dim = 256 scale_factor = 8.0 low_factor, high_factor = 1.0, 4.0 base_length = 8192 # Compute the inverse frequency based mostly on the usual RoPE formulation inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) # Compute the modified inverse frequency # scaled if freq too low, orig if freq too excessive, smoothed if in between wavelen = 2 * math.pi / inv_freq max_wavelen = base_length / low_factor min_wavelen = base_length / high_factor smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor) smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq new_freq = torch.the place(wavelen > max_wavelen, inv_freq / scale_factor, torch.the place(wavelen < min_wavelen, inv_freq, smoothed))
# Plot the ensuing inverse frequency plt.plot(inv_freq, label=‘Authentic’) plt.plot(inv_freq / scale_factor, label=‘Scaled’) plt.plot(new_freq, label=‘New Frequency’) plt.grid(True) plt.yscale(‘log’) plt.xlabel(‘Dimension’) plt.ylabel(‘Inverse Frequency’) plt.legend() plt.present() |
The plot is proven under:
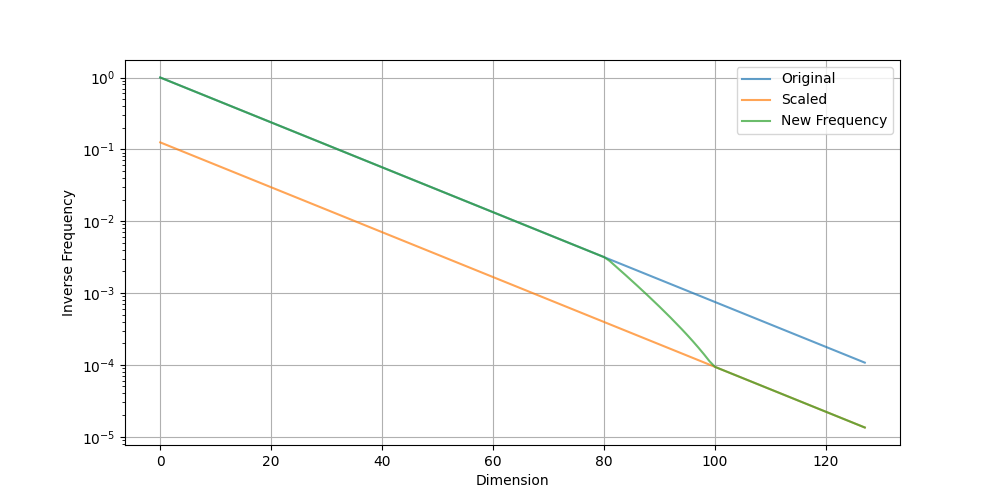
Plot of inverse frequency earlier than and after RoPE scaling
You possibly can see that the unique RoPE frequency is preserved till the wavelength is roughly 2000 tokens (at an inverse frequency of round 0.003), after which it’s step by step scaled. The wavelength is scaled by 8x when it exceeds 9000 tokens (the inverse frequency is under 6e-4).
From the x-axis of the plot, you’ll be able to see that round 60% of the scale seize dependencies inside 2000 tokens, whereas the remaining seize distances as much as 60000 tokens ($2pi N$ precisely; a bigger $N$ permits the mannequin to assist longer context lengths).
This successfully supplies the next decision for RoPE at quick distances and a decrease decision at lengthy distances, matching how language fashions ought to behave when understanding language.
Additional Studying
Beneath are some sources that you could be discover helpful:
Abstract
On this article, you discovered how RoPE is tailored for lengthy context size. Particularly, you discovered how Llama 3 helps longer context lengths by scaling the RoPE frequency on the low-frequency finish.
Rotary Place Embeddings (RoPE) is a method for encoding token positions in a sequence. It’s extensively utilized in many fashions and works properly for normal context lengths. Nevertheless, it requires adaptation for longer contexts. On this article, you’ll find out how RoPE is tailored for lengthy context size.
Let’s get began.

Rotary Place Embeddings for Lengthy Context Size
Picture by Nastya Dulhiier. Some rights reserved.
Overview
This text is split into two elements; they’re:
- Easy RoPE
- RoPE for Lengthy Context Size
Easy RoPE
In comparison with the sinusoidal place embeddings within the unique Transformer paper, RoPE mutates the enter tensor utilizing a rotation matrix:
$$
start{aligned}
X_{n,i} &= X_{n,i} cos(ntheta_i) – X_{n,frac{d}{2}+i} sin(ntheta_i)
X_{n,frac{d}{2}+i} &= X_{n,i} sin(ntheta_i) + X_{n,frac{d}{2}+i} cos(ntheta_i)
finish{aligned}
$$
the place $X_{n,i}$ is the $i$-th aspect of the vector on the $n$-th place of the sequence of tensor $X$. The size of every vector (also referred to as the hidden dimension or the mannequin dimension) is $d$. The amount $theta_i$ is the frequency of the $i$-th aspect of the vector. It’s computed as:
$$
theta_i = frac{1}{N^{2i/d}}
$$
A easy implementation of RoPE seems to be like this:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
import torch import torch.nn as nn
def rotate_half(x: torch.Tensor) -> torch.Tensor: “”“Rotates half the hidden dims of the enter.
It is a helper operate for rotary place embeddings (RoPE). For a tensor of form (…, d), it returns a tensor the place the final d/2 dimensions are rotated by swapping and negating.
Args: x: Enter tensor of form (…, d)
Returns: Tensor of similar form with rotated final dimension ““” x1, x2 = x.chunk(2, dim=–1) return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation
class RotaryPositionEncoding(nn.Module): “”“Rotary place encoding.”“”
def __init__(self, dim: int, max_position_embeddings: int) -> None: “”“Initialize the RotaryPositionEncoding module
Args: dim: The hidden dimension of the enter tensor to which RoPE is utilized max_position_embeddings: The utmost sequence size of the enter tensor ““” tremendous().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) place = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(place, inv_freq) # save cosine and sine matrices as buffers self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin())
def ahead(self, x: torch.Tensor) -> torch.Tensor: “”“Apply RoPE to tensor x
Args: x: Enter tensor of form (batch_size, seq_length, num_heads, head_dim)
Returns: Output tensor of form (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.form dtype = x.dtype # remodel the cosine and sine matrices to 4D tensor and the identical dtype as x cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x output = (x * cos) + (rotate_half(x) * sin) return output |
The code above defines a tensor inv_freq because the inverse frequency of the RoPE, comparable to the frequency time period $theta_i$ within the formulation. It’s referred to as inverse frequency within the RoPE literature as a result of it’s inversely proportional to the wavelength (i.e., the utmost distance) that RoPE can seize.
Once you multiply two vectors from positions $p$ and $q$, as you’ll do within the scaled-dot product consideration, you discover that the outcome relies on the relative place $p – q$ because of the trigonometric identities:
$$
start{aligned}
cos(a – b) = cos(a) cos(b) + sin(a) sin(b)
sin(a – b) = sin(a) cos(b) – cos(a) sin(b)
finish{aligned}
$$
In language fashions, relative place sometimes issues greater than absolute place. Due to this fact, RoPE is usually a more sensible choice than the unique sinusoidal place embeddings.
RoPE for Lengthy Context Size
The capabilities $sin kx$ and $cos kx$ are periodic with interval $2pi/okay$. In RoPE, the time period $theta_i$ is known as the frequency time period as a result of it determines the periodicity. In a language mannequin, the high-frequency phrases are vital as a result of they assist perceive close by phrases in a sentence. The low-frequency phrases, nevertheless, are helpful for understanding context that spans throughout a number of sentences.
Due to this fact, while you design a mannequin with an extended context size, you need it to carry out properly for brief sentences since they’re extra widespread, however you additionally need it to deal with lengthy contexts that your mannequin ought to assist. You do not need RoPE to deal with each sequence size equally.
The technique is to reallocate the RoPE scaling funds: apply a scaling issue to enhance long-range stability (at low frequencies of sine and cosine) whereas avoiding scaling when native place info is vital (at excessive frequencies of sine and cosine).
In Llama variations 1 and a pair of, RoPE is carried out with a most size of 4096, just like the earlier part. In Llama 3.1, the mannequin’s context size is expanded to 131K tokens, however RoPE is calculated utilizing a base size of 8192. The implementation is as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
import torch import torch.nn as nn import math
def rotate_half(x: Tensor) -> Tensor: “”“Rotates half the hidden dims of the enter.
It is a helper operate for rotary place embeddings (RoPE). For a tensor of form (…, d), it returns a tensor the place the final d/2 dimensions are rotated by swapping and negating.
Args: x: Enter tensor of form (…, d)
Returns: Tensor of similar form with rotated final dimension ““” x1, x2 = x.chunk(2, dim=–1) return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation
class RotaryPositionEncoding(nn.Module): “”“Rotary place encoding.”“”
def __init__(self, dim: int, max_position_embeddings: int, base_length: int = 8192) -> None: “”“Initialize the RotaryPositionEncoding module
Args: dim: The hidden dimension of the enter tensor to which RoPE is utilized max_position_embeddings: The utmost sequence size of the enter tensor base_length: The bottom size of the RoPE ““” tremendous().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 scale_factor = 8.0 low_factor, high_factor = 1.0, 4.0 base_length = 8192 # Compute the inverse frequency based mostly on the usual RoPE formulation inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float().to(“cuda”) / dim)) # Compute the modified inverse frequency # scaled if freq too low, orig if freq too excessive, smoothed if in between wavelen = 2 * math.pi / inv_freq max_wavelen = base_length / low_factor min_wavelen = base_length / high_factor smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor) smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq inv_freq = torch.the place(wavelen > max_wavelen, inv_freq / scale_factor, torch.the place(wavelen < min_wavelen, inv_freq, smoothed)) # multiply with sequence size inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) place = torch.arange(max_position_embeddings).float() sinusoid_inp = torch.outer(place, inv_freq) # save cosine and sine matrices as buffers self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin())
def ahead(self, x: Tensor) -> Tensor: “”“Apply RoPE to tensor x
Args: x: Enter tensor of form (batch_size, seq_length, num_heads, head_dim)
Returns: Output tensor of form (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.form dtype = x.dtype # remodel the cosine and sine matrices to 4D tensor and the identical dtype as x cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x output = (x * cos) + (rotate_half(x) * sin) return output |
The constructor of the RotaryPositionEncoding class makes use of a extra subtle algorithm to compute the inv_freq tensor. The thought is to compute a wavelength for every frequency part, which represents the utmost distance between two tokens that the actual RoPE part can seize. If the wavelength is just too quick (or the frequency is just too excessive), the frequency stays unchanged. Nevertheless, if the wavelength is just too lengthy, the frequency is scaled down by the scale_factor, successfully lengthening the utmost distance that RoPE part can seize. To make sure stability, frequency parts between the high and low frequency thresholds are easily interpolated.
As an example the impact of scaling, you’ll be able to plot the ensuing inverse frequency with Matplotlib:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
import matplotlib.pyplot as plt import torch import math
N = 10_000.0 dim = 256 scale_factor = 8.0 low_factor, high_factor = 1.0, 4.0 base_length = 8192 # Compute the inverse frequency based mostly on the usual RoPE formulation inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim)) # Compute the modified inverse frequency # scaled if freq too low, orig if freq too excessive, smoothed if in between wavelen = 2 * math.pi / inv_freq max_wavelen = base_length / low_factor min_wavelen = base_length / high_factor smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor) smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq new_freq = torch.the place(wavelen > max_wavelen, inv_freq / scale_factor, torch.the place(wavelen < min_wavelen, inv_freq, smoothed))
# Plot the ensuing inverse frequency plt.plot(inv_freq, label=‘Authentic’) plt.plot(inv_freq / scale_factor, label=‘Scaled’) plt.plot(new_freq, label=‘New Frequency’) plt.grid(True) plt.yscale(‘log’) plt.xlabel(‘Dimension’) plt.ylabel(‘Inverse Frequency’) plt.legend() plt.present() |
The plot is proven under:

Plot of inverse frequency earlier than and after RoPE scaling
You possibly can see that the unique RoPE frequency is preserved till the wavelength is roughly 2000 tokens (at an inverse frequency of round 0.003), after which it’s step by step scaled. The wavelength is scaled by 8x when it exceeds 9000 tokens (the inverse frequency is under 6e-4).
From the x-axis of the plot, you’ll be able to see that round 60% of the scale seize dependencies inside 2000 tokens, whereas the remaining seize distances as much as 60000 tokens ($2pi N$ precisely; a bigger $N$ permits the mannequin to assist longer context lengths).
This successfully supplies the next decision for RoPE at quick distances and a decrease decision at lengthy distances, matching how language fashions ought to behave when understanding language.
Additional Studying
Beneath are some sources that you could be discover helpful:
Abstract
On this article, you discovered how RoPE is tailored for lengthy context size. Particularly, you discovered how Llama 3 helps longer context lengths by scaling the RoPE frequency on the low-frequency finish.