A/B testing, also called break up testing, permits companies to experiment with completely different variations of a webpage or advertising and marketing asset to find out which one performs higher when it comes to person engagement, click-through charges, and, most significantly, conversion charges.
Conversion charges — the share of tourists who full a desired motion, equivalent to making a purchase order or signing up for a publication — are sometimes the important thing metrics that decide the success of on-line campaigns. By fastidiously testing variations of a webpage, companies could make data-driven selections that considerably enhance these charges. Whether or not it’s tweaking the colour of a call-to-action button, altering the headline, or rearranging the format, A/B testing offers actionable insights that may rework the effectiveness of your on-line presence.
On this publish, I’ll present do Bayesian A/B testing for conversion charges. We may even take a look at a extra difficult instance the place we’ll take a look at the variations in adjustments of buyer conduct after an intervention. We may even take a look at the variations when evaluating this strategy to a frequentist strategy and what the potential benefits or disadvantages are.
Let’s say we need to enhance upon our e-commerce web site. We achieve this by exposing two teams of shoppers to 2 variations of our web site the place we e.g. change a button. We then cease this experiment after having uncovered a sure variety of guests to each these variations. After that, we get a binary array with a 1 indicating conversion and a 0 if there was no conversion.
We are able to summarize the info in a contingency desk that exhibits us the (relative) frequencies.
contingency = np.array([[obsA.sum(), (1-obsA).sum()], [obsB.sum(), (1-obsB).sum()]])
In our case, we confirmed every variation to 100 prospects. Within the first variation, 5 (or 5%) transformed, and within the second variation 3 transformed.
Frequentist Setting
We’ll do a statistical check to measure if this result’s vital or as a result of likelihood. On this case, we’ll use a Chi2 check which compares the noticed frequencies to those that is perhaps anticipated if there have been no true variations between the 2 variations (the null speculation). For extra info, one can take a look at this weblog publish that goes into extra element.
On this case, the p-value doesn’t fall beneath the edge for significance (e.g. 5%) and subsequently we can not reject the null speculation that the 2 variants differ of their impact on the conversion fee.
Now, there are some pitfalls when utilizing the Chi2 check that may make the insights gained from it inaccurate. Firstly, it is vitally delicate to the pattern dimension. With a big pattern dimension even tiny variations will turn into vital whereas with a small pattern dimension, the check might fail to detect variations. That is particularly the case if the calculated anticipated frequencies for any of the fields are smaller than 5. On this case, one has to make use of another check. Moreover, the check doesn’t present info on the magnitude or sensible significance of the distinction. When conducting a number of A/B checks concurrently, the likelihood of discovering not less than one vital end result as a result of likelihood will increase. The Chi2 check doesn’t account for this a number of comparisons drawback, which might result in false positives if not correctly managed (e.g., via Bonferroni correction).
One other frequent pitfall happens when deciphering the outcomes of the Chi2 check (or any statistical check for that matter). The p-value provides us the likelihood of observing the info, on condition that the null speculation is true. It doesn’t make a press release concerning the distribution of conversion charges or their distinction. And this can be a main drawback. We can not make statements equivalent to “the likelihood that the conversion fee of variant B is 2% is X%” as a result of for that we would want the likelihood distribution of the conversion fee (conditioned on the noticed information).
These pitfalls spotlight the significance of understanding the constraints of the Chi2 check and utilizing it appropriately inside its constraints. When making use of this check, it’s essential to enrich it with different statistical strategies and contextual evaluation to make sure correct and significant conclusions.
Bayesian Setting
After trying on the frequentist approach of coping with A/B testing, let’s take a look at the Bayesian model. Right here, we’re modeling the data-generating course of (and subsequently the conversion fee) instantly. That’s, we’re specifying a probability and a previous that might result in the noticed end result. Consider this as specifying a ‘story’ for the way the info may have been created.
On this case, I’m utilizing the Python bundle PyMC for modeling because it has a transparent and concise syntax. Contained in the ‘with’ assertion, we specify distributions that we will mix and that give rise to a data-generating course of.
with pm.Mannequin() as ConversionModel:
# priors
pA = pm.Uniform('pA', 0, 1)
pB = pm.Uniform('pB', 0, 1)delta = pm.Deterministic('delta', pA - pB)
obsA = pm.Bernoulli('obsA', pA, noticed=obsA)
obsB = pm.Bernoulli('obsB', pB, noticed=obsB)
hint = pm.pattern(2000)
We’ve got pA and pB that are the possibilities of conversion in teams A and B respectively. With pm.Uniform we specify our prior perception about these parameters. That is the place we may encode prior information. In our case, we’re being impartial and permitting for any conversion fee between 0 and 1 to be equally seemingly.
PyMC then permits us to attract samples from the posterior distribution which is our up to date perception concerning the parameters after seeing the info. We now acquire a full likelihood distribution for the conversion chances.
From these distributions, we will instantly learn portions of curiosity equivalent to credible intervals. This permits us to reply questions equivalent to “What’s the probability of a conversion fee between X% and Y%?”.
The Bayesian strategy permits for far more flexibility as we’ll see later. Decoding the outcomes can also be extra simple and intuitive than within the frequentist setting.
We’ll now take a look at a extra difficult instance of A/B testing. Let’s say we expose topics to some intervention at first of the statement interval. This could be the A/B half the place one group will get intervention A and the opposite intervention B. We then take a look at the interplay of the two teams with our platform within the subsequent 100 days (perhaps one thing just like the variety of logins). What we’d see is the next.
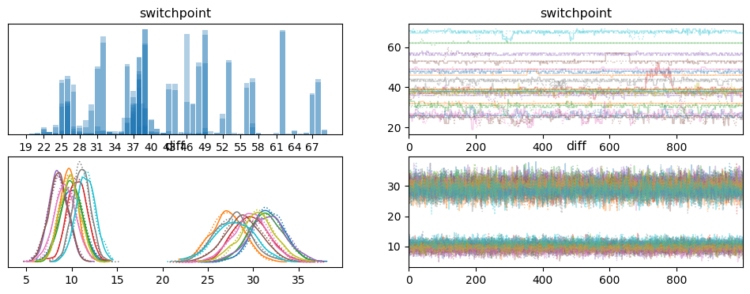
We now need to know if these two teams present a significant distinction of their response to the intervention. How would we clear up this with a statistical check? Frankly, I don’t know. Somebody must provide you with a statistical check for precisely this state of affairs. The choice is to once more come again to a Bayesian setting, the place we’ll first provide you with a data-generating course of. We’ll assume, that every particular person is impartial and its interactions with the platform are usually distributed. They’ve a swap level the place they alter their conduct. This swap level happens solely as soon as however can occur at any given cut-off date. Earlier than the swap level, we assume a imply interplay depth of mu1 and after that an depth of mu2. The syntax would possibly look a bit difficult particularly in case you have by no means used PyMC earlier than. In that case, I’d suggest testing their studying materials.
with pm.Mannequin(coords={
'ind_id': ind_id,
}) as SwitchPointModel:sigma = pm.HalfCauchy("sigma", beta=2, dims="ind_id")
# draw a switchpoint from a uniform distribution for every particular person
switchpoint = pm.DiscreteUniform("switchpoint", decrease=0, higher=100, dims="ind_id")
# priors for the 2 teams
mu1 = pm.HalfNormal("mu1", sigma=10, dims="ind_id")
mu2 = pm.HalfNormal("mu2", sigma=10, dims="ind_id")
diff = pm.Deterministic("diff", mu1 - mu2)
# create a deterministic variable for the
intercept = pm.math.swap(switchpoint < X.T, mu1, mu2)
obsA = pm.Regular("y", mu=intercept, sigma=sigma, noticed=obs)
hint = pm.pattern()
The mannequin can then present us the distribution for the swap level location in addition to the distribution of variations earlier than and after the swap level.
We are able to take a more in-depth take a look at these variations with a forest plot.
We are able to properly see how the variations between Group A (id 0 via 9) and Group B (10 via 19) are very a lot completely different the place group B exhibits a a lot higher response to the intervention.
Bayesian Inference presents loads of flexibility in the case of modeling conditions wherein we should not have loads of information and the place we care about modeling uncertainty. Moreover, we have now to make our assumptions express and take into consideration them. In additional easy eventualities, frequentist statistical checks are sometimes easier to make use of however one has to pay attention to the assumptions that come together with them.
All code used on this article will be discovered on my GitHub. Until in any other case said, all pictures are created by the writer.