For 18 days, we’ve explored a lot of the core machine studying fashions, organized into three main households: distance- and density-based fashions, tree- or rule-based fashions, and weight-based fashions.
Up thus far, every article targeted on a single mannequin, educated by itself. Ensemble studying adjustments this angle utterly. It’s not a standalone mannequin. As an alternative, it’s a method of combining these base fashions to construct one thing new.
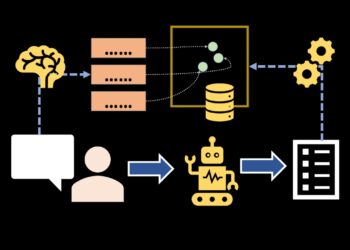
As illustrated within the diagram beneath, an ensemble is a meta-model. It sits on high of particular person fashions and aggregates their predictions.

Voting: the only ensemble concept
The best type of ensemble studying is voting.
The concept is nearly trivial: prepare a number of fashions, take their predictions, and compute the typical. If one mannequin is mistaken in a single course and one other is mistaken in the other way, the errors ought to cancel out. Not less than, that’s the instinct.
On paper, this sounds cheap. In observe, issues are very completely different.
As quickly as you attempt voting on actual fashions, one reality turns into apparent: voting shouldn’t be magic. Merely averaging predictions doesn’t assure higher efficiency. In lots of instances, it really makes issues worse.
The reason being easy. Whenever you mix fashions that behave very in a different way, you additionally mix their weaknesses. If the fashions don’t make complementary errors, averaging can dilute helpful construction as a substitute of reinforcing it.
To see this clearly, contemplate a quite simple instance. Take a call tree and a linear regression educated on the identical dataset. The choice tree captures native, non-linear patterns. The linear regression captures a worldwide linear development. Whenever you common their predictions, you don’t get hold of a greater mannequin. You get hold of a compromise that’s typically worse than every mannequin taken individually.

This illustrates an necessary level: ensemble studying requires greater than averaging. It requires a method. A method to mix fashions that truly improves stability or generalization.
Furthermore, if we contemplate the ensemble as a single mannequin, then it have to be educated as such. Easy averaging presents no parameter to regulate. There may be nothing to be taught, nothing to optimize.
One potential enchancment to voting is to assign completely different weights to the fashions. As an alternative of giving every mannequin the identical significance, we might attempt to be taught which of them ought to matter extra. However as quickly as we introduce weights, a brand new query seems: how will we prepare them? At that time, the ensemble itself turns into a mannequin that must be fitted.
This remark leads naturally to extra structured ensemble strategies.
On this article, we start with one statistical method to resample the coaching dataset earlier than averaging: Bagging.
The instinct behind Bagging
Why “bagging”?
What’s bagging?
The reply is definitely hidden within the title itself.
Bagging = Bootstrap + Aggregating.
You may instantly inform {that a} mathematician or a statistician named it. 🙂
Behind this barely intimidating phrase, the concept is very simple. Bagging is about doing two issues: first, creating many variations of the dataset utilizing the bootstrap, and second, aggregating the outcomes obtained from these datasets.
The core concept is due to this fact not about altering the mannequin. It’s about altering the information.
Bootstrapping the dataset
Bootstrapping means sampling the dataset with substitute. Every bootstrap pattern has the identical dimension as the unique dataset, however not the identical observations. Some rows seem a number of occasions. Others disappear.
In Excel, that is very straightforward to implement and, extra importantly, very straightforward to see.
You begin by including an ID column to your dataset, one distinctive identifier per row. Then, utilizing the RANDBETWEEN perform, you randomly draw row indices. Every draw corresponds to at least one row within the bootstrap pattern. By repeating this course of, you generate a full dataset that appears acquainted, however is barely completely different from the unique one.
This step alone already makes the concept of bagging concrete. You may actually see the duplicates. You may see which observations are lacking. Nothing is summary.
Under, you may see examples of bootstrap samples generated from the identical authentic dataset. Every pattern tells a barely completely different story, though all of them come from the identical information.
These various datasets are the inspiration of bagging.

Bagging linear regression: understanding the precept
Bagging course of
Sure, that is in all probability the primary time you hear about bagging linear regression.
In principle, there may be nothing mistaken with it. As we mentioned earlier, bagging is an ensemble technique that may be utilized to any base mannequin. Linear regression is a mannequin, so technically, it qualifies.
In observe, nonetheless, you’ll rapidly see that this isn’t very helpful.
However nothing prevents us from doing it. And exactly as a result of it’s not very helpful, it makes for a superb studying instance. So allow us to do it.
For every bootstrap pattern, we match a linear regression. In Excel, that is simple. We will immediately use the LINEST perform to estimate the coefficients. Every shade within the plot corresponds to at least one bootstrap pattern and its related regression line.
To date, every thing behaves precisely as anticipated. The traces are shut to one another, however not equivalent. Every bootstrap pattern barely adjustments the coefficients, and due to this fact the fitted line.

Now comes the important thing remark.
You might discover that one further mannequin is plotted in black. This one corresponds to the usual linear regression fitted on the authentic dataset, with out bootstrapping.
What occurs once we examine it to the bagged fashions?
Once we common the predictions of all these linear regressions, the ultimate result’s nonetheless a linear regression. The form of the prediction doesn’t change. The connection between the variables stays linear. We didn’t create a extra expressive mannequin.
And extra importantly, the bagged mannequin finally ends up being very near the usual linear regression educated on the unique information.
We will even push the instance additional by utilizing a dataset with a clearly non-linear construction. On this case, every linear regression fitted on a bootstrap pattern struggles in its personal method. Some traces tilt barely upward, others downward, relying on which observations have been duplicated or lacking within the pattern.

Bootstrap confidence intervals
From a prediction efficiency standpoint, bagging linear regression shouldn’t be very helpful.
Nevertheless, bootstrapping stays extraordinarily helpful for one necessary statistical notion: estimating the confidence interval of the predictions.
As an alternative of wanting solely on the common prediction, we will have a look at the distribution of predictions produced by all of the bootstrapped fashions. For every enter worth, we now have many predicted values, one from every bootstrap pattern.
A easy and intuitive method to quantify uncertainty is to compute the commonplace deviation of those predictions. This commonplace deviation tells us how delicate the prediction is to adjustments within the information. A small worth means the prediction is steady. A big worth means it’s unsure.
This concept works naturally in Excel. After getting all of the predictions from the bootstrapped fashions, computing their commonplace deviation is easy. The end result may be interpreted as a confidence band across the prediction.
That is clearly seen within the plot beneath. The interpretation is easy: in areas the place the coaching information is sparse or extremely dispersed, the boldness interval turns into broad, as predictions range considerably throughout bootstrap samples.
Conversely, the place the information is dense, predictions are extra steady and the boldness interval narrows.

Now, once we apply this to non-linear information, one thing turns into very clear. In areas the place the linear mannequin struggles to suit the information, the predictions from completely different bootstrap samples unfold out way more. The arrogance interval turns into wider.
This is a vital perception. Even when bagging doesn’t enhance prediction accuracy, it offers precious details about uncertainty. It tells us the place the mannequin is dependable and the place it’s not.
Seeing these confidence intervals emerge immediately from bootstrap samples in Excel makes this statistical idea very concrete and intuitive.

Bagging resolution bushes: from weak learners to a robust mannequin
Now we transfer to resolution bushes.
The precept of bagging stays precisely the identical. We generate a number of bootstrap samples, prepare one mannequin on every of them, after which combination their predictions.
I improved the Excel implementation to make the splitting course of extra computerized. To maintain issues manageable in Excel, we limit the bushes to a single cut up. Constructing deeper bushes is feasible, nevertheless it rapidly turns into cumbersome in a spreadsheet.
Under, you may see two of the bootstrapped bushes. In whole, I constructed eight of them by merely copying and pasting formulation, which makes the method simple and simple to breed.

Since resolution bushes are extremely non-linear fashions and their predictions are piecewise fixed, averaging their outputs has a smoothing impact.
Consequently, bagging naturally smooths the predictions. As an alternative of sharp jumps created by particular person bushes, the aggregated mannequin produces extra gradual transitions.
In Excel, this impact could be very straightforward to watch. The bagged predictions are clearly smoother than the predictions of any single tree.

A few of you could have already heard of resolution stumps, that are resolution bushes with a most depth of 1. That’s precisely what we use right here. Every mannequin is very simple. By itself, a stump is a weak learner.
The query right here is:
is a set of resolution stumps ample when mixed with bagging?
We are going to come again to this later in my Machine Studying “Introduction Calendar”.
Random Forest: extending bagging
What about Random Forest?
That is in all probability one of many favourite fashions amongst information scientists.
So why not speak about it right here, even in Excel?
The truth is, what we’ve simply constructed is already very near a Random Forest!
To know why, recall that Random Forest introduces two sources of randomness.
- The primary one is the bootstrap of the dataset. That is precisely what we’ve already accomplished with bagging.
- The second is randomness within the splitting course of. At every cut up, solely a random subset of options is taken into account.
In our case, nonetheless, we solely have one function. Which means there may be nothing to pick out from. Function randomness merely doesn’t apply.
Consequently, what we get hold of right here may be seen as a simplified Random Forest.
As soon as this idea is obvious, extending the concept to a number of options is simply a further layer of randomness, not a brand new idea.
And chances are you’ll even ask, we will apply this precept to Linear Regression, and do a Random
Conclusion
Ensemble studying is much less about advanced fashions and extra about managing instability.
Easy voting isn’t efficient. Bagging linear regression adjustments little and stays principally pedagogical, although it’s helpful for estimating uncertainty. With resolution bushes, nonetheless, bagging really issues: averaging unstable fashions results in smoother and extra sturdy predictions.
Random Forest naturally extends this concept by including additional randomness, with out altering the core precept. Seen in Excel, ensemble strategies cease being black packing containers and turn out to be a logical subsequent step.
Additional Studying
Thanks to your assist for my Machine Studying “Introduction Calendar“.
Folks normally speak loads about supervised studying, however unsupervised studying is usually ignored, though it will possibly reveal construction that no label might ever present.
If you wish to discover these concepts additional, listed below are three articles that dive into highly effective unsupervised fashions.
Gaussian Combination Mannequin
An improved and extra versatile model of k-means.
Not like k-means, GMM permits clusters to stretch, rotate, and adapt to the true form of the information.
However when do k-means and GMM really produce completely different outcomes?
Take a look at this text to see concrete examples and visible comparisons.
Native Outlier Issue (LOF)
A intelligent technique that compares every level’s native density to its neighbors to detect anomalies.
All of the Excel information can be found by means of this Kofi hyperlink. Your assist means loads to me. The value will enhance in the course of the month, so early supporters get the very best worth.