This text reveals how Shannon’s info idea connects to the instruments you’ll discover in trendy machine studying. We’ll tackle entropy and data achieve, then transfer to cross-entropy, KL divergence, and the strategies utilized in at the moment’s generative studying methods.
Right here’s what’s forward:
- Shannon’s core thought of quantifying info and uncertainty (bits) and why uncommon occasions carry extra info
- The development from entropy → info achieve/mutual info → cross-entropy and KL divergence
- How these concepts present up in observe: choice timber, function choice, classification losses, variational strategies, and InfoGAN

From Shannon to Fashionable AI: A Full Info Concept Information for Machine Studying
Picture by Creator
In 1948, Claude Shannon revealed a paper that modified how we take into consideration info eternally. His mathematical framework for quantifying uncertainty and shock grew to become the muse for the whole lot from knowledge compression to the loss features that practice at the moment’s neural networks.
Info idea offers you the mathematical instruments to measure and work with uncertainty in knowledge. When you choose options for a mannequin, optimize a neural community, or construct a choice tree, you’re making use of ideas Shannon developed over 75 years in the past. This information connects Shannon’s authentic insights to the knowledge idea ideas you employ in machine studying at the moment.
What Shannon Found
Shannon’s breakthrough was to deal with info as one thing you could possibly really measure. Earlier than 1948, info was qualitative — you both had it otherwise you didn’t. Shannon confirmed that info may very well be quantified mathematically by uncertainty and shock.
The basic precept is elegant: uncommon occasions carry extra info than frequent occasions. Studying that it rained within the desert tells you greater than studying the solar rose this morning. This relationship between chance and data content material grew to become the muse for measuring uncertainty in knowledge.
Shannon captured this relationship in a easy mathematical components:
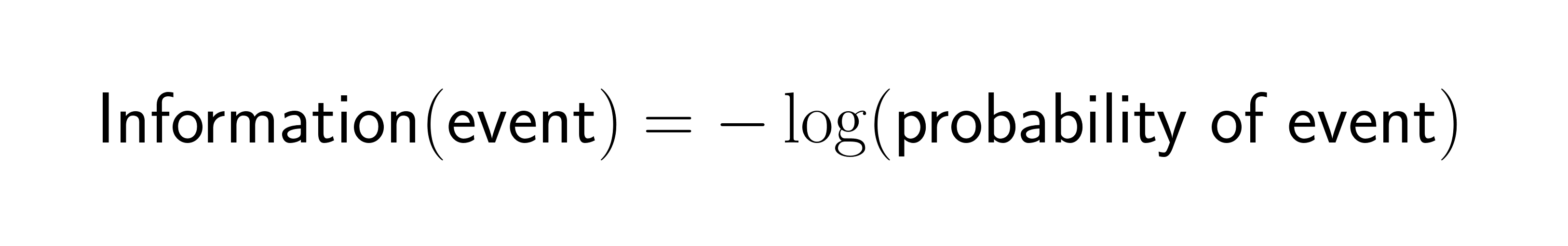
When an occasion has chance 1.0 (certainty), it offers you zero info. When an occasion is extraordinarily uncommon, it offers excessive info content material. This inverse relationship drives most info idea functions in machine studying.
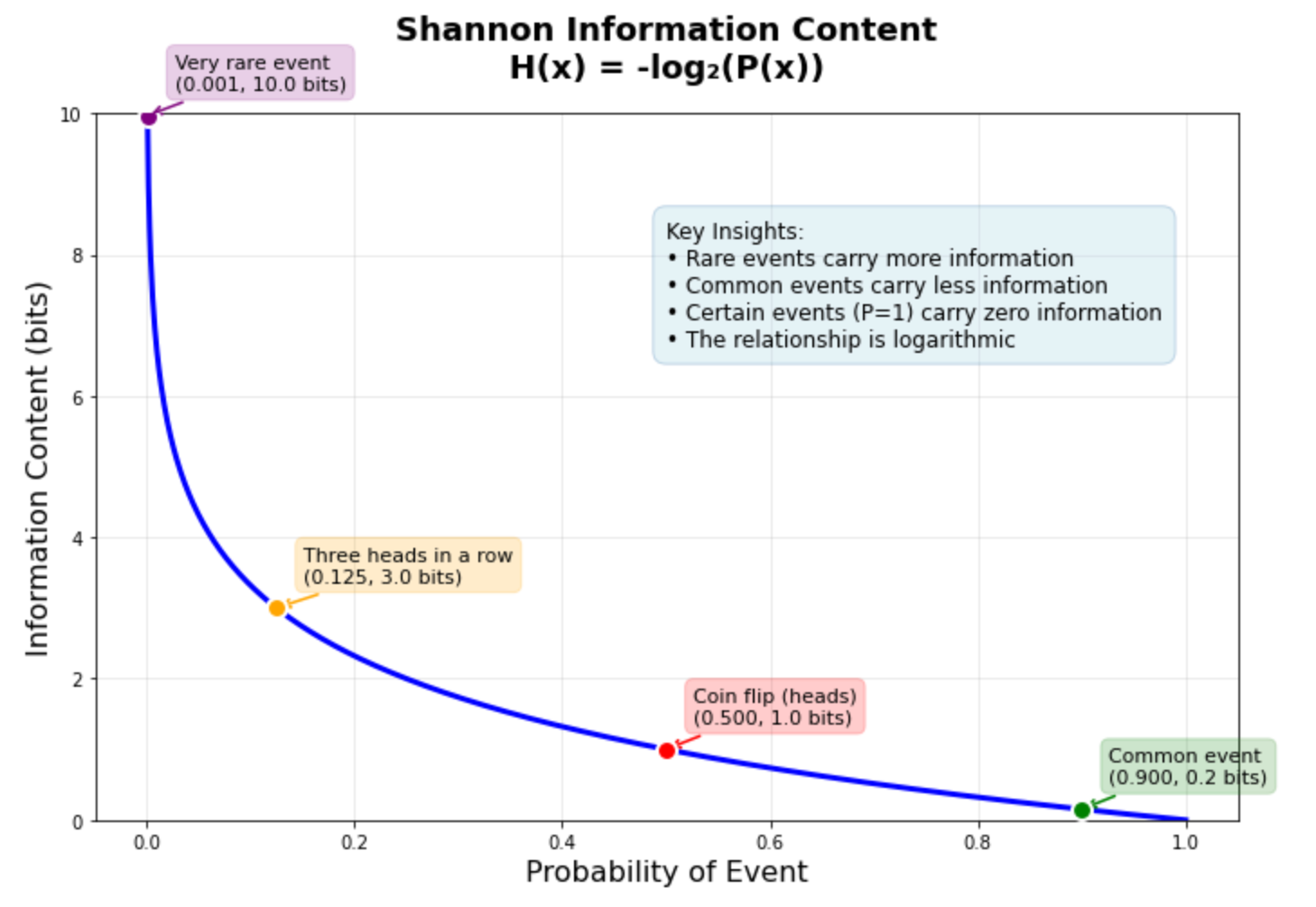
The graph above reveals this relationship in motion. A coin flip (50% chance) carries precisely 1 bit of data. Getting three heads in a row (12.5% chance) carries 3 bits. A really uncommon occasion with 0.1% chance carries about 10 bits — roughly ten instances extra info than the coin flip. This logarithmic relationship helps clarify why machine studying fashions usually battle with uncommon occasions: they carry a lot info that the mannequin wants many examples to be taught dependable patterns.
Constructing the Mathematical Basis: Entropy
Shannon prolonged his info idea to total chance distributions by entropy. Entropy measures the anticipated info content material when sampling from a chance distribution.
For a distribution with equally doubtless outcomes, entropy reaches its most — there’s excessive uncertainty about which occasion will happen. For skewed distributions the place one final result dominates, entropy is decrease as a result of the dominant final result is predictable.
This is applicable on to machine studying datasets. A wonderfully balanced binary classification dataset has most entropy, whereas an imbalanced dataset has decrease entropy as a result of one class is extra predictable than the opposite.
For the whole mathematical derivation, step-by-step calculations, and Python implementations, see A Light Introduction to Info Entropy. This tutorial offers labored examples and implementations from scratch.
From Entropy to Info Achieve
Shannon’s entropy idea leads naturally to info achieve, which measures how a lot uncertainty decreases while you be taught one thing new. Info achieve calculates the discount in entropy while you cut up knowledge in keeping with some criterion.
This precept drives choice tree algorithms. When constructing a choice tree, algorithms like ID3 and CART consider potential splits by calculating info achieve. The cut up that provides you the largest discount in uncertainty will get chosen.
Info achieve additionally extends to function choice by mutual info. Mutual info measures how a lot realizing one variable tells you about one other variable. Options with excessive mutual info relative to the goal variable are extra informative for prediction duties.
The mathematical relationship between entropy, info achieve, and mutual info, together with labored examples and Python code, is defined intimately in Info Achieve and Mutual Info for Machine Studying. This tutorial offers step-by-step calculations displaying precisely how info achieve guides choice tree splitting.
Cross-Entropy As a Loss Operate
Shannon’s info idea ideas discovered direct software in machine studying by cross-entropy loss features. Cross-entropy measures the distinction between predicted chance distributions and true distributions.
When coaching classification fashions, cross-entropy loss quantifies how a lot info is misplaced when utilizing predicted chances as an alternative of true chances. Fashions that predict chance distributions nearer to the true distribution have decrease cross-entropy loss.
This connection between info idea and loss features isn’t coincidental. Cross-entropy loss emerges naturally from most chance estimation, which seeks to search out mannequin parameters that make the noticed knowledge most possible beneath the mannequin.
Cross-entropy grew to become the usual loss perform for classification duties as a result of it offers robust gradients when predictions are assured however unsuitable, serving to fashions be taught quicker. The mathematical foundations, implementation particulars, and relationship to info idea are lined totally in A Light Introduction to Cross-Entropy for Machine Studying.
Measuring Distribution Variations: KL Divergence
Constructing on cross-entropy ideas, the Kullback-Leibler (KL) divergence offers you a strategy to measure how a lot one chance distribution differs from one other. KL divergence quantifies the extra info wanted to signify knowledge utilizing an approximate distribution as an alternative of the true distribution.
Not like cross-entropy, which measures coding price relative to the true distribution, KL divergence measures the additional info price of utilizing an imperfect mannequin. This makes KL divergence significantly helpful for evaluating fashions or measuring how effectively one distribution approximates one other.
KL divergence seems all through machine studying in variational inference, generative fashions, and regularization methods. It offers a principled strategy to penalize fashions that deviate too removed from prior beliefs or reference distributions.
The mathematical foundations of KL divergence, its relationship to cross-entropy and entropy, plus implementation examples are detailed in Learn how to Calculate the KL Divergence for Machine Studying. This tutorial additionally covers the associated Jensen-Shannon divergence and reveals implement each measures in Python.
Info Concept in Fashionable AI
Fashionable AI functions prolong Shannon’s ideas in refined methods. Generative adversarial networks (GANs) use info idea ideas to be taught knowledge distributions, with discriminators performing information-theoretic comparisons between actual and generated knowledge.
The Info Maximizing GAN (InfoGAN) explicitly incorporates mutual info into the coaching goal. By maximizing mutual info between latent codes and generated photos, InfoGAN learns disentangled representations the place totally different latent variables management totally different points of generated photos.
Transformer architectures, the muse of contemporary language fashions, could be understood by info idea lenses. Consideration mechanisms route info based mostly on relevance, and the coaching course of learns to compress and remodel info throughout layers.
Info bottleneck idea offers one other trendy perspective, suggesting that neural networks be taught by compressing inputs whereas preserving info related to the duty. This view helps clarify why deep networks generalize effectively regardless of their excessive capability.
A whole implementation of InfoGAN with detailed explanations of how mutual info is integrated into GAN coaching is supplied in Learn how to Develop an Info Maximizing GAN (InfoGAN) in Keras.
Constructing Your Info Concept Toolkit
Understanding when to use totally different info idea ideas improves your machine studying observe. Right here’s a framework for selecting the best device:
Use entropy when it’s good to measure uncertainty in a single distribution. This helps consider dataset stability, assess prediction confidence, or design regularization phrases that encourage various outputs.
Use info achieve or mutual info when choosing options or constructing choice timber. These measures establish which variables provide the most details about your goal variable.
Use cross-entropy when coaching classification fashions. Cross-entropy loss offers good gradients and connects on to most chance estimation ideas.
Use KL divergence when evaluating chance distributions or implementing variational strategies. KL divergence measures distribution variations in a principled means that respects the probabilistic construction of your downside.
Use superior functions like InfoGAN when it’s good to be taught structured representations or need specific management over info stream in generative fashions.
This development strikes from measuring uncertainty in knowledge (entropy) to optimizing fashions (cross-entropy). Superior functions embody evaluating distributions (KL divergence) and studying structured representations (InfoGAN).
Subsequent Steps
The 5 tutorials linked all through this information present complete protection of data idea for machine studying. They progress from primary entropy ideas by functions to superior methods like InfoGAN.
Begin with the entropy tutorial to construct instinct for info content material and uncertainty measurement. Transfer by info achieve and mutual info to grasp function choice and choice timber. Research cross-entropy to grasp trendy loss features, then discover KL divergence for distribution comparisons. Lastly, study InfoGAN to see how info idea ideas apply to generative fashions.
Every tutorial consists of full Python implementations, labored examples, and functions. Collectively, they provide you a whole basis for making use of info idea ideas in your machine studying initiatives.
Shannon’s 1948 insights proceed to drive improvements in synthetic intelligence. Understanding these ideas and their trendy functions offers you entry to a mathematical framework that explains why many machine studying methods work and apply them extra successfully.
This text reveals how Shannon’s info idea connects to the instruments you’ll discover in trendy machine studying. We’ll tackle entropy and data achieve, then transfer to cross-entropy, KL divergence, and the strategies utilized in at the moment’s generative studying methods.
Right here’s what’s forward:
- Shannon’s core thought of quantifying info and uncertainty (bits) and why uncommon occasions carry extra info
- The development from entropy → info achieve/mutual info → cross-entropy and KL divergence
- How these concepts present up in observe: choice timber, function choice, classification losses, variational strategies, and InfoGAN

From Shannon to Fashionable AI: A Full Info Concept Information for Machine Studying
Picture by Creator
In 1948, Claude Shannon revealed a paper that modified how we take into consideration info eternally. His mathematical framework for quantifying uncertainty and shock grew to become the muse for the whole lot from knowledge compression to the loss features that practice at the moment’s neural networks.
Info idea offers you the mathematical instruments to measure and work with uncertainty in knowledge. When you choose options for a mannequin, optimize a neural community, or construct a choice tree, you’re making use of ideas Shannon developed over 75 years in the past. This information connects Shannon’s authentic insights to the knowledge idea ideas you employ in machine studying at the moment.
What Shannon Found
Shannon’s breakthrough was to deal with info as one thing you could possibly really measure. Earlier than 1948, info was qualitative — you both had it otherwise you didn’t. Shannon confirmed that info may very well be quantified mathematically by uncertainty and shock.
The basic precept is elegant: uncommon occasions carry extra info than frequent occasions. Studying that it rained within the desert tells you greater than studying the solar rose this morning. This relationship between chance and data content material grew to become the muse for measuring uncertainty in knowledge.
Shannon captured this relationship in a easy mathematical components:
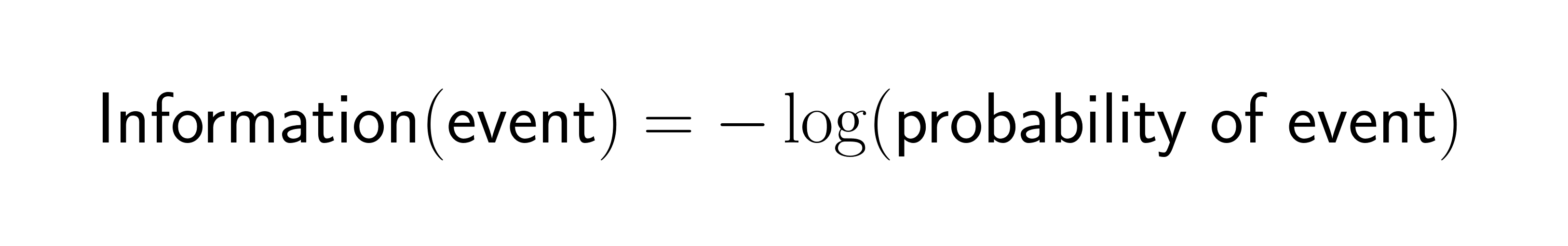
When an occasion has chance 1.0 (certainty), it offers you zero info. When an occasion is extraordinarily uncommon, it offers excessive info content material. This inverse relationship drives most info idea functions in machine studying.

The graph above reveals this relationship in motion. A coin flip (50% chance) carries precisely 1 bit of data. Getting three heads in a row (12.5% chance) carries 3 bits. A really uncommon occasion with 0.1% chance carries about 10 bits — roughly ten instances extra info than the coin flip. This logarithmic relationship helps clarify why machine studying fashions usually battle with uncommon occasions: they carry a lot info that the mannequin wants many examples to be taught dependable patterns.
Constructing the Mathematical Basis: Entropy
Shannon prolonged his info idea to total chance distributions by entropy. Entropy measures the anticipated info content material when sampling from a chance distribution.
For a distribution with equally doubtless outcomes, entropy reaches its most — there’s excessive uncertainty about which occasion will happen. For skewed distributions the place one final result dominates, entropy is decrease as a result of the dominant final result is predictable.
This is applicable on to machine studying datasets. A wonderfully balanced binary classification dataset has most entropy, whereas an imbalanced dataset has decrease entropy as a result of one class is extra predictable than the opposite.
For the whole mathematical derivation, step-by-step calculations, and Python implementations, see A Light Introduction to Info Entropy. This tutorial offers labored examples and implementations from scratch.
From Entropy to Info Achieve
Shannon’s entropy idea leads naturally to info achieve, which measures how a lot uncertainty decreases while you be taught one thing new. Info achieve calculates the discount in entropy while you cut up knowledge in keeping with some criterion.
This precept drives choice tree algorithms. When constructing a choice tree, algorithms like ID3 and CART consider potential splits by calculating info achieve. The cut up that provides you the largest discount in uncertainty will get chosen.
Info achieve additionally extends to function choice by mutual info. Mutual info measures how a lot realizing one variable tells you about one other variable. Options with excessive mutual info relative to the goal variable are extra informative for prediction duties.
The mathematical relationship between entropy, info achieve, and mutual info, together with labored examples and Python code, is defined intimately in Info Achieve and Mutual Info for Machine Studying. This tutorial offers step-by-step calculations displaying precisely how info achieve guides choice tree splitting.
Cross-Entropy As a Loss Operate
Shannon’s info idea ideas discovered direct software in machine studying by cross-entropy loss features. Cross-entropy measures the distinction between predicted chance distributions and true distributions.
When coaching classification fashions, cross-entropy loss quantifies how a lot info is misplaced when utilizing predicted chances as an alternative of true chances. Fashions that predict chance distributions nearer to the true distribution have decrease cross-entropy loss.
This connection between info idea and loss features isn’t coincidental. Cross-entropy loss emerges naturally from most chance estimation, which seeks to search out mannequin parameters that make the noticed knowledge most possible beneath the mannequin.
Cross-entropy grew to become the usual loss perform for classification duties as a result of it offers robust gradients when predictions are assured however unsuitable, serving to fashions be taught quicker. The mathematical foundations, implementation particulars, and relationship to info idea are lined totally in A Light Introduction to Cross-Entropy for Machine Studying.
Measuring Distribution Variations: KL Divergence
Constructing on cross-entropy ideas, the Kullback-Leibler (KL) divergence offers you a strategy to measure how a lot one chance distribution differs from one other. KL divergence quantifies the extra info wanted to signify knowledge utilizing an approximate distribution as an alternative of the true distribution.
Not like cross-entropy, which measures coding price relative to the true distribution, KL divergence measures the additional info price of utilizing an imperfect mannequin. This makes KL divergence significantly helpful for evaluating fashions or measuring how effectively one distribution approximates one other.
KL divergence seems all through machine studying in variational inference, generative fashions, and regularization methods. It offers a principled strategy to penalize fashions that deviate too removed from prior beliefs or reference distributions.
The mathematical foundations of KL divergence, its relationship to cross-entropy and entropy, plus implementation examples are detailed in Learn how to Calculate the KL Divergence for Machine Studying. This tutorial additionally covers the associated Jensen-Shannon divergence and reveals implement each measures in Python.
Info Concept in Fashionable AI
Fashionable AI functions prolong Shannon’s ideas in refined methods. Generative adversarial networks (GANs) use info idea ideas to be taught knowledge distributions, with discriminators performing information-theoretic comparisons between actual and generated knowledge.
The Info Maximizing GAN (InfoGAN) explicitly incorporates mutual info into the coaching goal. By maximizing mutual info between latent codes and generated photos, InfoGAN learns disentangled representations the place totally different latent variables management totally different points of generated photos.
Transformer architectures, the muse of contemporary language fashions, could be understood by info idea lenses. Consideration mechanisms route info based mostly on relevance, and the coaching course of learns to compress and remodel info throughout layers.
Info bottleneck idea offers one other trendy perspective, suggesting that neural networks be taught by compressing inputs whereas preserving info related to the duty. This view helps clarify why deep networks generalize effectively regardless of their excessive capability.
A whole implementation of InfoGAN with detailed explanations of how mutual info is integrated into GAN coaching is supplied in Learn how to Develop an Info Maximizing GAN (InfoGAN) in Keras.
Constructing Your Info Concept Toolkit
Understanding when to use totally different info idea ideas improves your machine studying observe. Right here’s a framework for selecting the best device:
Use entropy when it’s good to measure uncertainty in a single distribution. This helps consider dataset stability, assess prediction confidence, or design regularization phrases that encourage various outputs.
Use info achieve or mutual info when choosing options or constructing choice timber. These measures establish which variables provide the most details about your goal variable.
Use cross-entropy when coaching classification fashions. Cross-entropy loss offers good gradients and connects on to most chance estimation ideas.
Use KL divergence when evaluating chance distributions or implementing variational strategies. KL divergence measures distribution variations in a principled means that respects the probabilistic construction of your downside.
Use superior functions like InfoGAN when it’s good to be taught structured representations or need specific management over info stream in generative fashions.
This development strikes from measuring uncertainty in knowledge (entropy) to optimizing fashions (cross-entropy). Superior functions embody evaluating distributions (KL divergence) and studying structured representations (InfoGAN).
Subsequent Steps
The 5 tutorials linked all through this information present complete protection of data idea for machine studying. They progress from primary entropy ideas by functions to superior methods like InfoGAN.
Begin with the entropy tutorial to construct instinct for info content material and uncertainty measurement. Transfer by info achieve and mutual info to grasp function choice and choice timber. Research cross-entropy to grasp trendy loss features, then discover KL divergence for distribution comparisons. Lastly, study InfoGAN to see how info idea ideas apply to generative fashions.
Every tutorial consists of full Python implementations, labored examples, and functions. Collectively, they provide you a whole basis for making use of info idea ideas in your machine studying initiatives.
Shannon’s 1948 insights proceed to drive improvements in synthetic intelligence. Understanding these ideas and their trendy functions offers you entry to a mathematical framework that explains why many machine studying methods work and apply them extra successfully.