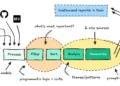
artificial information era, we usually create a mannequin for our actual (or ‘noticed’) information, after which use this mannequin to generate artificial information. This noticed information is often compiled from actual world experiences, akin to measurements of the bodily traits of irises or particulars about people who’ve defaulted on credit score or acquired some medical situation. We are able to consider the noticed information as having come from some ‘father or mother distribution’ — the true underlying distribution from which the noticed information is a random pattern. In fact, we by no means know this father or mother distribution — it have to be estimated, and that is the aim of our mannequin.
However if our mannequin can produce artificial information that may be thought of to be a random pattern from the identical father or mother distribution, then we’ve hit the jackpot: the artificial information will possess the identical statistical properties and patterns because the noticed information (constancy); will probably be simply as helpful when put to duties akin to regression or classification (utility); and, as a result of it’s a random pattern, there isn’t any danger of it figuring out the noticed information (privateness). However how can we all know if we now have met this elusive objective?
Within the first a part of this story, we’ll conduct some easy experiments to achieve a greater understanding of the issue and inspire an answer. Within the second half we’ll consider efficiency of quite a lot of artificial information turbines on a set of well-known datasets.
Half 1 — Some Easy Experiments
Think about the next two datasets and attempt to reply this query:
Are the datasets random samples from the identical father or mother distribution, or has one been derived from the opposite by making use of small random perturbations?

The datasets clearly show related statistical properties, akin to marginal distributions and covariances. They might additionally carry out equally on a classification process during which a classifier educated on one dataset is examined on the opposite.
However suppose we had been to plot the information factors from every dataset on the identical graph. If the datasets are random samples from the identical father or mother distribution, we might intuitively count on the factors from one dataset to be interspersed with these from the opposite in such a way that, on common, factors from one set are as near — or ‘as much like’ — their closest neighbors in that set as they’re to their closest neighbors within the different set. Nevertheless, if one dataset is a slight random perturbation of the opposite, then factors from one set shall be extra much like their closest neighbors within the different set than they’re to their closest neighbors in the identical set. This results in the next check.
The Most Similarity Take a look at
For every dataset, calculate the similarity between every occasion and its closest neighbor within the similar dataset. Name these the ‘most intra-set similarities’. If the datasets have the identical distributional traits, then the distribution of intra-set similarities ought to be related for every dataset. Now calculate the similarity between every occasion of 1 dataset and its closest neighbor within the different dataset and name these the ‘most cross-set similarities’. If the distribution of most cross-set similarities is similar because the distribution of most intra-set similarities, then the datasets may be thought of random samples from the identical father or mother distribution. For the check to be legitimate, every dataset ought to include the identical variety of examples.

Because the datasets we cope with on this story all include a combination of numerical and categorical variables, we’d like a similarity measure which may accommodate this. We use Gower Similarity¹.
The desk and histograms beneath present the means and distributions of the utmost intra- and cross-set similarities for Datasets 1 and a couple of.


On common, the situations in one information set are extra much like their closest neighbors within the different dataset than they’re to their closest neighbors in the identical dataset. This means that the datasets usually tend to be perturbations of one another than random samples from the identical father or mother distribution. And certainly, they’re perturbations! Dataset 1 was generated from a Gaussian combination mannequin; Dataset 2 was generated by choosing (with out substitute) an occasion from Dataset 1 and making use of a small random perturbation.
Finally, we shall be utilizing the Most Similarity Take a look at to match artificial datasets with noticed datasets. The most important hazard with artificial information factors being too near noticed factors is privateness; i.e., with the ability to establish factors within the noticed set from factors within the artificial set. Actually, if you happen to look at Datasets 1 and a couple of fastidiously, you would possibly really be capable to establish some such pairs. And that is for a case during which the common most cross-set similarity is barely 0.3% bigger than the common most intra-set similarity!
Modeling and Synthesizing
To finish this primary a part of the story, let’s create a mannequin for a dataset and use the mannequin to generate artificial information. We are able to then use the Most Similarity Take a look at to match the artificial and noticed units.
The dataset on the left of Determine 4 beneath is simply Dataset 1 from above. The dataset on the fitting (Dataset 3) is the artificial dataset. (We’ve estimated the distribution as a Gaussian combination, however that’s not vital).

Listed below are the common similarities and histograms:


The three averages are an identical to 3 important figures, and the three histograms are very related. Subsequently, based on the Most Similarity Take a look at, each datasets can fairly be thought of random samples from the identical father or mother distribution. Our artificial information era train has been successful, and we now have achieved the trifecta — constancy, utility, and privateness.
[Python code used to produce the datasets, plots and histograms from Part 1 is available from https://github.com/a-skabar/TDS-EvalSynthData]
Half 2— Actual Datasets, Actual Mills
The dataset used in Half 1 is easy and may be simply modeled with only a combination of Gaussians. Nevertheless, most real-world datasets are way more complicated. On this a part of the story, we’ll apply a number of artificial information turbines to some well-liked real-world datasets. Our main focus is on evaluating the distributions of most similarities inside and between the noticed and artificial datasets to grasp the extent to which they are often thought of random samples from the identical father or mother distribution.
The six datasets originate from the UCI repository² and are all well-liked datasets which have been broadly used within the machine studying literature for many years. All are mixed-type datasets, and had been chosen as a result of they fluctuate of their stability of categorical and numerical options.
The six turbines are consultant of the main approaches utilized in artificial information era: copula-based, GAN-based, VAE-based, and approaches utilizing sequential imputation. CopulaGAN³, GaussianCopula, CTGAN³ and TVAE³ are all out there from the Artificial Information Vault libraries⁴, synthpop⁵ is accessible as an open-source R bundle, and ‘UNCRi’ refers back to the artificial information era software developed underneath the Unified Numeric/Categorical Illustration and Inference (UNCRi) framework⁶. All turbines had been used with their default settings.
Desk 1 exhibits the common most intra- and cross-set similarities for every generator utilized to every dataset. Entries highlighted in purple are these during which privateness has been compromised (i.e., the common most cross-set similarity exceeds the common most intra-set similarity on the noticed information). Entries highlighted in inexperienced are these with the highest common most cross-set similarity (not together with these in purple). The final column exhibits the results of performing a Prepare on Artificial, Take a look at on Actual (TSTR) check, the place a classifier or regressor is educated on the artificial examples and examined on the actual (noticed) examples. The Boston Housing dataset is a regression process, and the imply absolute error (MAE) is reported; all different duties are classification duties, and the reported worth is the world underneath ROC curve (AUC).

The figures beneath show, for every dataset, the distributions of most intra- and cross-set similarities similar to the generator that attained the very best common most cross-set similarity (excluding these highlighted in purple above).






From the desk, we are able to see that for these turbines that didn’t breach privateness, the common most cross-set similarity may be very near the common most intra-set similarity on noticed information. The histograms present us the distributions of those most similarities, and we are able to see that most often the distributions are clearly related — strikingly so for datasets such because the Census Earnings dataset. The desk additionally exhibits that the generator that achieved the very best common most cross-set similarity for every dataset (excluding these highlighted in purple) additionally demonstrated finest efficiency on the TSTR check (once more excluding these in purple). Thus, whereas we are able to by no means declare to have found the ‘true’ underlying distribution, these outcomes reveal that the simplest generator for every dataset has captured the essential options of the underlying distribution.
Privateness
Solely two of the seven turbines displayed points with privateness: synthpop and TVAE. Every of those breached privateness on three out of the six datasets. In two situations, particularly TVAE on Cleveland Coronary heart Illness and TVAE on Credit score Approval, the breach was significantly extreme. The histograms for TVAE on Credit score Approval are proven beneath and reveal that the artificial examples are far too related to one another, and likewise to their closest neighbors within the noticed information. The mannequin is a very poor illustration of the underlying father or mother distribution. The rationale for this can be that the Credit score Approval dataset comprises a number of numerical options which are extraordinarily extremely skewed.

Different observations and feedback
The 2 GAN-based turbines — CopulaGAN and CTGAN — had been constantly among the many worst performing turbines. This was considerably shocking given the immense recognition of GANs.
The efficiency of GaussianCopula was mediocre on all datasets besides Wisconsin Breast Most cancers, for which it attained the equal-highest common most cross-set similarity. Its unimpressive efficiency on the Iris dataset was significantly shocking, on condition that it is a quite simple dataset that may simply be modeled utilizing a combination of Gaussians, and which we anticipated can be well-matched to Copula-based strategies.
The turbines which carry out most constantly properly throughout all datasets are synthpop and UNCRi, which each function by sequential imputation. Because of this they solely ever must estimate and pattern from a univariate conditional distribution (e.g., P(x₇|x₁, x₂, …)), and that is usually a lot simpler than modeling and sampling from a multivariate distribution (e.g., P(x₁, x₂, x₃, …)), which is (implicitly) what GANs and VAEs do. Whereas synthpop estimates distributions utilizing resolution timber (that are the supply of the overfitting that synthpop is vulnerable to), the UNCRi generator estimates distributions utilizing a nearest neighbor-based method, with hyper-parameters optimized utilizing a cross-validation process that stops overfitting.
Conclusion
Artificial information era is a brand new and evolving subject, and whereas there are nonetheless no commonplace analysis methods, there may be consensus that checks ought to cowl constancy, utility and privateness. However whereas every of those is vital, they don’t seem to be on an equal footing. For instance, an artificial dataset could obtain good efficiency on constancy and utility however fail on privateness. This doesn’t give it a ‘two out of three’: if the artificial examples are too near the noticed examples (thus failing the privateness check), the mannequin has been overfitted, rendering the constancy and utility checks meaningless. There was a bent amongst some distributors of artificial information era software program to suggest single-score measures of efficiency that mix outcomes from a mess of checks. That is primarily primarily based on the identical ‘two out of three’ logic.
If an artificial dataset may be thought of a random pattern from the identical father or mother distribution because the noticed information, then we can’t do any higher — we now have achieved most constancy, utility and privateness. The Most Similarity Take a look at gives a measure of the extent to which two datasets may be thought of random samples from the identical father or mother distribution. It’s primarily based on the easy and intuitive notion that if an noticed and an artificial dataset are random samples from the identical father or mother distribution, situations ought to be distributed such {that a} artificial occasion is as related on common to its closest noticed occasion as an noticed occasion is analogous on common to its closest noticed occasion.
We suggest the next single-score measure of artificial dataset high quality:

The nearer this ratio is to 1 — with out exceeding 1 — the higher the standard of the artificial information. It ought to, in fact, be accompanied by a sanity examine of the histograms.
References
[1] Gower, J. C. (1971). A common coefficient of similarity and a few of its properties. Biometrics, 27(4), 857–871.
[2] Dua, D. & Graff, C., (2017). UCI Machine Studying Repository, Accessible at: http://archive.ics.uci.edu/ml.
[3] Xu, L., Skoularidou, M., Cuesta-Infante, A. and Veeramachaneni., Okay. Modeling Tabular information utilizing Conditional GAN. NeurIPS, 2019.
[4] Patki, N., Wedge, R., & Veeramachaneni, Okay. (2016). The artificial information vault. In 2016 IEEE Worldwide Convention on Information Science and Superior Analytics (DSAA) (pp. 399–410). IEEE.
[5] Nowok, B., Raab G.M., Dibben, C. (2016). “synthpop: Bespoke Creation of Artificial Information in R.” Journal of Statistical Software program, 74(11), 1–26.
[6] http://skanalytix.com/uncri-framework
[7] Harrison, D., & Rubinfeld, D.L. (1978). Boston Housing Dataset. Kaggle. https://www.kaggle.com/c/boston-housing. Licensed for business use underneath the CC: Public Area license.
[8] Kohavi, R. (1996). Census Earnings. UCI Machine Studying Repository. archive.ics.uci.edu/dataset/20/census+earnings. Licensed for business use underneath a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.
[9] Janosi, A., Steinbrunn, W., Pfisterer, M. and Detrano, R. (1988). Coronary heart Illness. UCI Machine Studying Repository. archive.ics.uci.edu/dataset/45/coronary heart+illness. Licensed for business use underneath a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.
[10] Quinlan, J.R. (1987). Credit score Approval. UCI Machine Studying Repository. archive.ics.uci.edu/dataset/27/credit score+approval. Licensed for business use underneath a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.
[11] Fisher, R.A. (1988). Iris. UCI Machine Studying Repository. archive.ics.uci.edu/dataset/53/iris. Licensed for business use underneath a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.
[12] Wolberg, W., Mangasarian, O., Avenue, N. and Avenue,W. (1995). Breast Most cancers Wisconsin (Diagnostic). UCI Machine Studying Repository. archive.ics.uci.edu/dataset/17/breast+most cancers+wisconsin+diagnostic. Licensed for business use underneath a Inventive Commons Attribution 4.0 Worldwide (CC BY 4.0) license.