In fashions, the unbiased variables should be not or solely barely depending on one another, i.e. that they don’t seem to be correlated. Nevertheless, if such a dependency exists, that is known as Multicollinearity and results in unstable fashions and outcomes which might be tough to interpret. The variance inflation issue is a decisive metric for recognizing multicollinearity and signifies the extent to which the correlation with different predictors will increase the variance of a regression coefficient. A excessive worth of this metric signifies a excessive correlation of the variable with different unbiased variables within the mannequin.
Within the following article, we glance intimately at multicollinearity and the VIF as a measurement instrument. We additionally present how the VIF might be interpreted and what measures might be taken to scale back it. We additionally examine the indicator with different strategies for measuring multicollinearity.
What’s Multicollinearity?
Multicollinearity is a phenomenon that happens in regression evaluation when two or extra variables are strongly correlated with one another so {that a} change in a single variable results in a change within the different variable. Because of this, the event of an unbiased variable might be predicted fully or at the very least partially by one other variable. This complicates the prediction of linear regression to find out the affect of an unbiased variable on the dependent variable.
A distinction might be made between two sorts of multicollinearity:
- Good Multicollinearity: a variable is an actual linear mixture of one other variable, for instance when two variables measure the identical factor in several models, akin to weight in kilograms and kilos.
- Excessive Diploma of Multicollinearity: Right here, one variable is strongly, however not fully, defined by at the very least one different variable. For instance, there’s a excessive correlation between an individual’s schooling and their earnings, however it’s not good multicollinearity.
The prevalence of multicollinearity in regressions results in critical issues as, for instance, the regression coefficients turn into unstable and react very strongly to new information, in order that the general prediction high quality suffers. Numerous strategies can be utilized to acknowledge multicollinearity, such because the correlation matrix or the variance inflation issue, which we are going to have a look at in additional element within the subsequent part.
What’s the Variance Inflation Issue (VIF)?
The variance inflation issue (VIF) describes a diagnostic instrument for regression fashions that helps to detect multicollinearity. It signifies the issue by which the variance of a coefficient will increase because of the correlation with different variables. A excessive VIF worth signifies a powerful multicollinearity of the variable with different unbiased variables. This negatively influences the regression coefficient estimate and leads to excessive commonplace errors. It’s subsequently necessary to calculate the VIF in order that multicollinearity is acknowledged at an early stage and countermeasures might be taken. :
[] [VIF = frac{1}{(1 – R^2)}]
Right here (R^2) is the so-called coefficient of dedication of the regression of function (i) towards all different unbiased variables. A excessive (R^2) worth signifies that a big proportion of the variables might be defined by the opposite options, in order that multicollinearity is suspected.
In a regression with the three unbiased variables (X_1), (X_2) and (X_3), for instance, one would prepare a regression with (X_1) because the dependent variable and (X_2) and (X_3) as unbiased variables. With the assistance of this mannequin, (R_{1}^2) may then be calculated and inserted into the formulation for the VIF. This process would then be repeated for the remaining mixtures of the three unbiased variables.
A typical threshold worth is VIF > 10, which signifies robust multicollinearity. Within the following part, we glance in additional element on the interpretation of the variance inflation issue.
How can totally different Values of the Variance Inflation Issue be interpreted?
After calculating the VIF, it is very important be capable of consider what assertion the worth makes in regards to the scenario within the mannequin and to have the ability to deduce whether or not measures are mandatory. The values might be interpreted as follows:
- VIF = 1: This worth signifies that there isn’t any multicollinearity between the analyzed variable and the opposite variables. Which means no additional motion is required.
- VIF between 1 and 5: If the worth is within the vary between 1 and 5, then there’s multicollinearity between the variables, however this isn’t giant sufficient to signify an precise drawback. Fairly, the dependency continues to be reasonable sufficient that it may be absorbed by the mannequin itself.
- VIF > 5: In such a case, there’s already a excessive diploma of multicollinearity, which requires intervention in any case. The usual error of the predictor is prone to be considerably extreme, so the regression coefficient could also be unreliable. Consideration needs to be given to combining the correlated predictors into one variable.
- VIF > 10: With such a worth, the variable has critical multicollinearity and the regression mannequin may be very prone to be unstable. On this case, consideration needs to be given to eradicating the variable to acquire a extra highly effective mannequin.
Total, a excessive VIF worth signifies that the variable could also be redundant, as it’s extremely correlated with different variables. In such circumstances, varied measures needs to be taken to scale back multicollinearity.
What measures assist to scale back the VIF?
There are numerous methods to avoid the consequences of multicollinearity and thus additionally cut back the variance inflation issue. The preferred measures embody:
- Eradicating extremely correlated variables: Particularly with a excessive VIF worth, eradicating particular person variables with excessive multicollinearity is an efficient instrument. This will enhance the outcomes of the regression, as redundant variables estimate the coefficients extra unstable.
- Principal part evaluation (PCA): The core thought of principal part evaluation is that a number of variables in an information set could measure the identical factor, i.e. be correlated. Which means the assorted dimensions might be mixed into fewer so-called principal elements with out compromising the importance of the info set. Peak, for instance, is very correlated with shoe dimension, as tall individuals typically have taller sneakers and vice versa. Which means the correlated variables are then mixed into uncorrelated predominant elements, which reduces multicollinearity with out dropping necessary info. Nevertheless, that is additionally accompanied by a lack of interpretability, because the principal elements don’t signify actual traits, however a mix of various variables.
- Regularization Strategies: Regularization includes varied strategies which might be utilized in statistics and machine studying to regulate the complexity of a mannequin. It helps to react robustly to new and unseen information and thus permits the generalizability of the mannequin. That is achieved by including a penalty time period to the mannequin’s optimization perform to forestall the mannequin from adapting an excessive amount of to the coaching information. This strategy reduces the affect of extremely correlated variables and lowers the VIF. On the identical time, nonetheless, the accuracy of the mannequin will not be affected.
These strategies can be utilized to successfully cut back the VIF and fight multicollinearity in a regression. This makes the outcomes of the mannequin extra steady and the usual error might be higher managed.
How does the VIF examine to different strategies?
The variance inflation issue is a extensively used approach to measure multicollinearity in an information set. Nevertheless, different strategies can supply particular benefits and drawbacks in comparison with the VIF, relying on the applying.
Correlation Matrix
The correlation matrix is a statistical methodology for quantifying and evaluating the relationships between totally different variables in an information set. The pairwise correlations between all mixtures of two variables are proven in a tabular construction. Every cell within the matrix accommodates the so-called correlation coefficient between the 2 variables outlined within the column and the row.
This worth might be between -1 and 1 and supplies info on how the 2 variables relate to one another. A constructive worth signifies a constructive correlation, that means that a rise in a single variable results in a rise within the different variable. The precise worth of the correlation coefficient supplies info on how strongly the variables transfer about one another. With a unfavorable correlation coefficient, the variables transfer in reverse instructions, that means that a rise in a single variable results in a lower within the different variable. Lastly, a coefficient of 0 signifies that there isn’t any correlation.
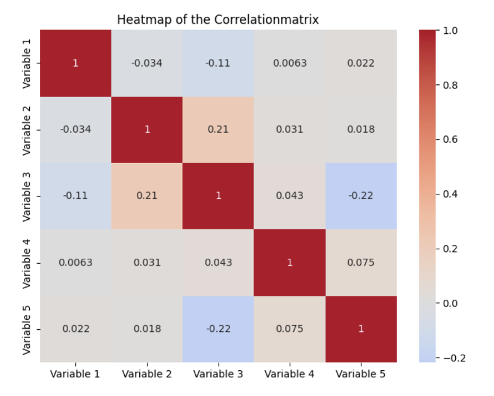
A correlation matrix subsequently fulfills the aim of presenting the correlations in an information set in a fast and easy-to-understand manner and thus kinds the premise for subsequent steps, akin to mannequin choice. This makes it potential, for instance, to acknowledge multicollinearity, which may trigger issues with regression fashions, because the parameters to be discovered are distorted.
In comparison with the VIF, the correlation matrix solely presents a floor evaluation of the correlations between variables. Nevertheless, the largest distinction is that the correlation matrix solely reveals the pairwise comparisons between variables and never the simultaneous results between a number of variables. As well as, the VIF is extra helpful for quantifying precisely how a lot multicollinearity impacts the estimate of the coefficients.
Eigenvalue Decomposition
Eigenvalue decomposition is a technique that builds on the correlation matrix and mathematically helps to establish multicollinearity. Both the correlation matrix or the covariance matrix can be utilized. Normally, small eigenvalues point out a stronger, linear dependency between the variables and are subsequently an indication of multicollinearity.
In comparison with the VIF, the eigenvalue decomposition presents a deeper mathematical evaluation and may in some circumstances additionally assist to detect multicollinearity that may have remained hidden by the VIF. Nevertheless, this methodology is far more advanced and tough to interpret.
The VIF is an easy and easy-to-understand methodology for detecting multicollinearity. In comparison with different strategies, it performs properly as a result of it permits a exact and direct evaluation that’s on the stage of the person variables.
How one can detect Multicollinearity in Python?
Recognizing multicollinearity is a vital step in information preprocessing in machine studying to coach a mannequin that’s as significant and strong as potential. On this part, we subsequently take a more in-depth have a look at how the VIF might be calculated in Python and the way the correlation matrix is created.
Calculating the Variance Inflation Think about Python
The Variance Inflation Issue might be simply used and imported in Python through the statsmodels library. Assuming we have already got a Pandas DataFrame in a variable X that accommodates the unbiased variables, we will merely create a brand new, empty DataFrame for calculating the VIFs. The variable names and values are then saved on this body.

A brand new row is created for every unbiased variable in X within the Variable column. It’s then iterated via all variables within the information set and the variance inflation issue is calculated for the values of the variables and once more saved in a listing. This checklist is then saved as column VIF within the DataFrame.
Calculating the Correlation Matrix
In Python, a correlation matrix might be simply calculated utilizing Pandas after which visualized as a heatmap utilizing Seaborn. For example this, we generate random information utilizing NumPy and retailer it in a DataFrame. As quickly as the info is saved in a DataFrame, the correlation matrix might be created utilizing the corr() perform.
If no parameters are outlined inside the perform, the Pearson coefficient is utilized by default to calculate the correlation matrix. In any other case, you can too outline a distinct correlation coefficient utilizing the strategy parameter.

Lastly, the heatmap is visualized utilizing seaborn. To do that, the heatmap() perform is named and the correlation matrix is handed. Amongst different issues, the parameters can be utilized to find out whether or not the labels needs to be added and the colour palette might be specified. The diagram is then displayed with the assistance of matplolib.
That is what you must take with you
- The variance inflation issue is a key indicator for recognizing multicollinearity in a regression mannequin.
- The coefficient of dedication of the unbiased variables is used for the calculation. Not solely the correlation between two variables might be measured, but additionally mixtures of variables.
- Normally, a response needs to be taken if the VIF is larger than 5, and acceptable measures needs to be launched. For instance, the affected variables might be faraway from the info set or the principal part evaluation might be carried out.
- In Python, the VIF might be calculated immediately utilizing statsmodels. To do that, the info should be saved in a DataFrame. The correlation matrix will also be calculated utilizing Seaborn to detect multicollinearity.




















