The Animated Monte-Carlo Tree Search (MCTS) | by Thomas Kurbiel | Jan, 2025

The algorithm on the coronary heart of AlphaGo, AlphaGo Zero, AlphaZero and MuZero

Monte-Carlo Tree Search (MCTS) is a heuristic search technique, whose important function is to decide on essentially the most promising transfer, given the present state of a sport. It does so via repeatedly enjoying the sport ranging from the present state, thus figuring out promising strikes and rapidly abandoning the unpromising ones. As we are going to shortly see, the problem lies in performing as little play-outs as doable, whereas wanting forward into the longer term so far as doable. MCTS is the important thing algorithm behind many main achievements in current AI purposes such because the spectacular AlphaGo showdown in 2016, the place AlphaGo outplayed the second-highest ranked Go participant.

At first look MCTS might seem as a easy algorithm, nevertheless it includes a excessive stage of hidden complexity, equivalent to an inherent “exploitation-exploration trade-off”. Because of the extremely dynamic nature of the algorithm — the search tree grows and is up to date on every iteration — it’s best defined utilizing animations, a variety of animations. It will allow you to to rapidly develop a stable psychological idea of MCTS, making it a lot simpler to know groundbreaking advances just like the well-known AlphaGo, the place MCTS is mixed with neural networks.

On this article, we are going to begin with the motivation behind MCTS. Subsequent, we are going to introduce all the only steps the algorithm is made from: choice, growth, simulation and backpropagation. We take a very shut take a look at the backpropagation, as it’s uncared for in lots of tutorials. Lastly, we are going to take a really shut take a look at the mechanism behind the “exploitation-exploration trade-off”.

We’re going to use a deterministic model of the well-known setting grid world to get conversant in MCTS. On this model the agent precisely obeys our instructions with out slipping to the edges randomly:

As you possibly can see from the animation, we will select from the 4 completely different compass instructions (North, West, South, East). There are two closing states: a winner state with a reward of +1 and a loser state with a reward of -1. All different states return a small destructive reward of -0.02, which discourages wandering round aimlessly and that encourages taking the shortest route. The black cell is an impediment and the agent can’t undergo this cell.

If the agent bounces off the wall, it simply stays the place it’s, nevertheless accumulating a destructive reward of -0.02.

On the finish of this put up we are going to lengthen the grid world to have stochastic dynamics: below these circumstances, if we command the agent to go north, there’s, for instance, a ten% likelihood that it’s going to unintentionally gear off to the left and a ten% likelihood that it’s going to gear off to the best, and solely a 80% likelihood that it’s going to handle to go the course we commanded.

Final however not least, as a planning algorithm MCTS does require the setting to have the ability to retailer a state and to load a state, such that we will carry out a number of play-outs, ranging from the identical state.

As a facet word: the grid world is a small instance of what’s known as a Markov determination course of (MDP).

Our objective is to seek out the quickest path to the constructive reward within the higher proper nook of the grid world. We’ll first devise a easy brute-force algorithm, which systematically tries out all doable mixtures of actions.

First discover, how the illustration of all of the doable future states naturally results in a tree-like construction. Every node of the tree represents a specific state within the sport, whereas edges characterize completely different actions. The kid nodes of every node therefore characterize all doable subsequent states a participant can attain from there. The terminal states of the sport are represented by leaf nodes and don’t possess any kids. The node on the high known as root node.

Please discover the hierarchical group of the tree: the basis node belongs to stage 0, its youngster nodes belong to stage 1 and their kids in flip belong to stage 2 and so forth. Furthermore, every stage represents a unique future time limit: stage 0 represents the present step, stage 1 represents all doable future states after taking a single motion, stage 2 characterize all doable future states after taking two actions and so forth.

Now, we discover an fascinating factor: the complete rewards (the numbers beneath every node) in all ranges explored to date are equivalent. Specifically, this implies, that even after reaching stage 2, we nonetheless can’t determine which motion to take subsequent. Thus, we have to broaden the tree a lot deeper:

We see within the left a part of the determine above, that by both taking the “up” or “proper” motion within the root state, we will attain the winner state in 5 steps. The maximal doable reward quantities to 0.92. Taking the “down” or “left” motion, depicted on the right-hand facet of the determine, entails not less than one bump towards a wall, solely permitting the agent to achieve the winner state at stage 6 with the ultimate reward decreased to 0.9.

We are able to conclude that increasing the tree in depth is essential for correct decision-making. The flip facet of the coin nevertheless is, that the quantity of states we have to go to rises exponentially with every further stage:

• At stage 1: 4
• At stage 2: 4² = 16
• At stage 3: 4³ = 64
• At stage 4: 4⁴ = 256
• At stage 5: 4⁵ = 1024
• …
• At stage 10: 4¹⁰ = 1.048.576

The 4 used above is the so known as branching issue and corresponds to the variety of actions we will soak up every state. Go has a branching issue of roughly 250 (!!!), whereas chess sometimes has round 30 actions to select from. Increasing simply 5 steps forward in Go, leads us to an astronomical variety of doable states: 250⁵ = 976.562.500.000.

Visiting each node of the search tree is impractical, particularly since for correct determination making we should broaden the tree in depth to look additional forward into the longer term. However how can we make the brute-force tree-search algorithm above possible for extra advanced duties?

The answer that MCTS pursues, is to run repeated simulations known as roll-outs or play-outs. In every play-out, the sport is performed out to the very finish by choosing strikes at random. The ultimate sport result’s used to rapidly establish and abandon unpromising paths and solely consider the extra promising ones.

The whole reward we get hold of within the roll-out depicted above quantities to 0.62. Bear in mind, that the shortest paths we explored earlier than yielded a complete reward of 0.92. We therefore see a excessive variance within the outcomes of various simulations. So as to acquire confidence in regards to the statistics, we have to repeatedly runs simulations within the setting. This repeated random sampling of the search tree is what’s implied by the title Monte-Carlo.

One final comment concerning the second phrase “tree-search” in MCTS: keep in mind that the systematic traversal of a tree with the intention to discover an optimum path known as: tree-search.

The very first thing we do is to reset the setting with the intention to begin from a managed state. We than save the state (it’s truly a checkpoint which totally describes the preliminary state of the setting). Subsequently, we create a brand new search tree node and append the simply obtained state to it:

As now we have seen within the introduction, a search tree is a hierarchical construction, the place every node will be related to many kids, however have to be related to precisely one dad or mum, apart from the basis node, which has no dad or mum. An summary information sort representing a node should therefore hold an inventory with tips that could the kid nodes and a pointer to the dad or mum node. Different vital member variables of the node construction are:

• reward: reward for taking motion a in state s
• value_sum: sum of all obtained worth estimates
  (see definition of worth beneath)
• visit_count: what number of play-outs contribute to value_sum
• state: checkpoint describing the complete state of the setting

As well as we are going to hold an inventory of all but unvisited actions and a boolean variable indicating whether or not the state is terminal or not.

We begin by loading the state related to the basis node into the setting. Subsequent, we decide an unexplored motion from the set of unvisited actions. We step the setting utilizing the simply picked motion and word down returned values equivalent to reward, finished, and many others.

Just like the initialization step, we then load the brand new state from the setting, create a brand new search tree node and join it to the state. Lastly, we populate the reward member variable (and possibly different variables) with the simply obtained values. Final however not least, we add a pointer from the basis to the newly created youngster node and the pointer from the kid node to the dad or mum.

Please word, that within the MCTS model introduced on this tutorial, we broaden solely a single node earlier than persevering with with the simulation step. Different flavors of MCTS would possibly broaden all youngster nodes first, earlier than persevering with with the simulation steps.

The principle function of the simulation step is to acquire an estimate of how promising the at the moment visited state is. Bear in mind, that we outline the notion of “how good” a state is, when it comes to the cumulative reward that’s anticipated to be collected from that state on, going into the longer term:

The cumulative reward, additionally known as return, is calculated for the trajectory obtained throughout a random roll-out:

which begins at present state at timestep t, is performed to the very finish of the sport, i.e. till a terminal state is reached, and whose actions are taken in keeping with a random roll-out coverage.

It’s common to make use of a reduction issue 𝛾 ∈ (0, 1) to provide extra weight to rapid rewards than to rewards acquired additional into the longer term:

Moreover, utilizing a reduction issue prevents the full reward from going to infinity for longer roll-outs (would you quite obtain $1000 at present or $1000 ten years from now?).

The above worth is calculated on a single roll-out and will differ quite a bit relying on the randomly chosen actions (we are saying: it has high-variance). To achieve confidence in regards to the statistics, we should due to this fact common over a number of roll-outs:

The expression above known as value-function within the literature: it’s merely the anticipated sum of discounted future rewards, when beginning in state t and following coverage π thereafter.

Please word, that the anticipated return, in fact depends upon the particular coverage the agent is following, which is indicated by π within the subscript of the expectation operator. On the whole value-functions will not be solely calculated for random insurance policies, however for arbitrary insurance policies.

Now, allow us to come again to the operating instance:

For comfort we use a gamma issue 𝛾 = 1.0. The very first thing we do is load the state related to the “up” youngster node into the setting. Then we play the sport to the very finish utilizing the random roll-out coverage. Lastly, we word down the obtained return.

First discover that the time period backpropagate is somewhat deceptive, because it has nothing to do with the backpropagation utilized in neural networks to compute the gradients.

The principle function of the backpropagation step is to recursively replace the worth estimates of all nodes mendacity alongside the trail from root to the simply visited leaf node. The replace is carried out ranging from the underside of the search tree all the way in which as much as the basis. The entity being backpropagated is the worth estimate obtained within the final simulation.

Please discover somewhat peculiarity: the reward with index t is definitely granted for taking the “down” motion in state t:

In our implementation it’s nevertheless related to the state at time t+1. This can be a deliberate alternative as a result of this fashion we solely need to hold a single reward per node. Alternatively, we must hold an inventory of 4 rewards (belonging to every motion) within the state at time t.

Allow us to subsequent derive the recursive components: assume now we have obtained an estimate of the worth for the state at timestep t+1 by rolling out a random coverage:

To get the estimate for the state at timestep t, we simply want so as to add the earlier reward to the above expression:

In fact, now we have to think about the low cost issue. The proof of the above expression may be very easy: simply plug within the first equation above into the second:

An identical recursive components can also be obtainable for the value-function:

which we nevertheless gained’t derive on this put up. By the way in which, the above components known as Bellman equation and is the muse of many RL algorithms.

Now, allow us to come again to the operating instance:

The very first thing we do, is so as to add the estimate (worth = 0.64) obtained within the simulation step to value_sum:

Subsequent, we improve the visit_count:

This fashion, we hold observe on what number of play-outs our worth estimate is predicated. Final however not least, we apply the above recursive components to acquire a worth estimate for the basis node.

Thus far, now we have seen the next steps of the MCTS algorithm: growth, simulation and backpropagation. To wrap our data, allow us to repeat all of the steps for the kid node belonging to the “proper” motion:

The play-out carried out within the simulation step occurs to finish up within the purple loser state after taking 8 actions, yielding a destructive worth estimate of -1.16.

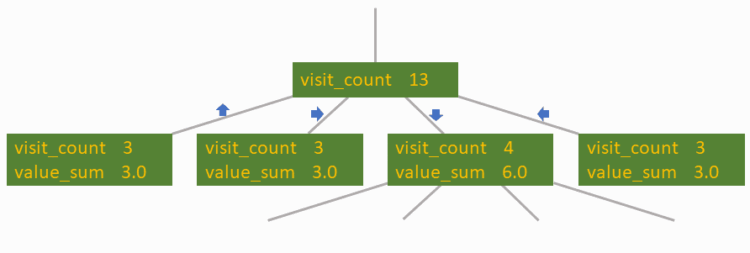
The final step we have to carry out is to backpropagate. Please word, how the visit_count of the basis node is at all times equivalent to the sum of the visit_counts of its youngster nodes.

The very same technique of increasing, simulating and backpropagating is repeated for the remaining unvisited actions of the basis node: “down” and “left”. For the reason that process needs to be clear by now, we skip the corresponding animations.

We arrive on the level the place all youngster nodes of the basis have been expanded and a single simulation has been run on every considered one of them. The foundation is totally expanded now:

The query arises as to which of the kid nodes we should always choose for additional exploration. Bear in mind, the objective of MCTS is to concentrate on promising paths, whereas rapidly abandoning unpromising ones. The components that satisfies all these circumstances known as UCT (Higher Confidence Sure 1 utilized to bushes):

We apply the above components to every of the kid nodes and choose the kid node with the very best UCT worth. The primary a part of the components is solely the estimate of the value-function, we’ve launched in a earlier part, and displays “how promising” the related state is. The second a part of the components represents a bonus for not often visited youngster nodes. We’ll see in a later part, that the primary half corresponds to what’s known as exploitation, and the second half to what’s known as exploration.

Subsequent, let’s plug all of the values from the above determine into the UCT components utilizing c = 1.2:

The kid node belonging to the “up” motion is the most effective youngster and is chosen. Let’s proceed with the animation:

Let’s rapidly recap what we all know in regards to the choice step: its important function is to seek out essentially the most promising path from the basis node to a leaf node utilizing the UCT components. To this finish, we begin on the high of the search tree and utilizing UCT choose the most effective youngster in stage 1. Relying on the depth of the tree, we then proceed with stage 2 performing once more UCT and choosing its greatest youngster. We repeat this process, till we attain a not (!) totally expanded node (aka leaf node) or a terminal node.

As soon as we attain a not totally expanded node (a leaf node that also has unvisited actions), we then proceed with the Simulation and Backpropagation steps. Do not forget that throughout Backpropagation all of the value_sums and visit_counts alongside the trail to the leaf node are up to date. Within the subsequent iteration, we begin once more from the basis node and use UCT to establish essentially the most promising path.

Take into account that this path might differ considerably from the earlier iteration because of the updates made over the last Backpropagation step: plugging the numbers from the final body of the above animation

provides us the next UCT values for the basis node:

This time the kid node belonging to the “left” motion is chosen.

The Enlargement step, as launched above, refers solely to choosing one of many unvisited actions and including the corresponding youngster node to the tree. Nevertheless, within the following, we are going to use the time period broaden a node to collectively discuss with the three steps: Enlargement, Simulation, and Backpropagation.

The 2 distinct steps of choice and growth are oftentimes summarized below the time period tree-policy:

On this part we are going to clarify the mechanism behind the UCT components intimately. For illustrative functions we begin with an already constructed up search tree. The node depicted beneath is totally expanded (has 4 youngster nodes) and is situated someplace in, say, stage 4.

First, allow us to take a look on the visit_count of its youngster nodes. We see, that the “down” motion was visited 4 instances, whereas the others have been visited solely 3 instances. If we examine the value_sum of every node, we discover that the worth related to the “down” motion is twice as giant.

Now, dividing the value_sum by the visit_count provides us an estimate of how promising every state is:

Now, with the intention to choose the most effective youngster, we may simply go for the very best worth above. In different phrases, we have already got acquired some data about how promising every state is, and now we simply need to “exploit” that data.

Nevertheless, there’s a hazard with this technique: please keep in mind, that we use random simulations to acquire the estimates and people will be very noisy generally. A promising state may therefore simply find yourself getting a low worth estimate and vice versa. Simply choosing a state, which solely by likelihood obtained a excessive worth, would utterly cease additional exploration for extra promising paths.

For precisely this cause the UCT components has a second time period, which we are going to analyze subsequent:

Allow us to first take a fast look, at similar traversals going via our dad or mum node:

For illustrative functions, all of the numbers within the instance above have been chosen such that when utilizing the UCT components with c = 1.2, the “down” motion is chosen 5 instances in a row.

Now, whenever you look rigorously, you’ll discover, that in every backpropagation step the visit_count of the chosen youngster node is incremented by one, whereas the visit_count of the remaining youngster nodes stays unchanged. Moreover, the visit_count of the dad or mum node can also be incremented by one, because the backpropagations path at all times leads via it.

Subsequent, allow us to plot the “exploration” a part of the UCB components for all 4 youngster nodes:

We see, that the worth is rising for all non-selected youngster nodes. That is logical, since their visit_count showing within the denominator stays fixed, whereas the dad or mum’s visit_count within the nominator is incremented. In distinction, for the chosen “down” node, the worth is reducing. Right here the log of the visit_count of the dad or mum node is rising slower that the “unlogged” visit_count of the kid nodes. Now, we see, that there should exist a future time limit, the place the “exploration” a part of the unvisited nodes has grown so giant, such that they’ll ultimately be revisited once more.

This mechanism ensures “exploration” so that each from time to time paths that don’t look very promising at first are however explored sooner or later and will change into very promising. With out this mechanism MCTS would utterly disregarding paths that haven’t but been explored. Exploration by UCB takes into consideration the variety of instances every motion was chosen, and provides further weight to the less-explored. The parameter c permits us to trade-off between “exploration” and “exploitation”.

Allow us to rapidly recap what defines a deterministic setting: we begin from a specific state of our sport and take an motion, that teleports us to the subsequent state. Now, we reset the setting to the identical authentic state and repeat the identical motion. In a deterministic setting we at all times find yourself within the precisely similar subsequent state. Nevertheless, in stochastic environments, the subsequent state we find yourself in is unsure.

The most important adaptation now we have to use to MCTS, when coping with stochastic environments, is the choice step. Bear in mind, within the choice step we use the tree coverage to assemble a path from the basis to most promising leaf node. Alongside the discovered path now we have a specific sequence of actions.

Within the deterministic case, beginning within the root state and making use of this sequence of actions would at all times lead us to precisely the identical states alongside the trail. Within the stochastic case, the visited states may nevertheless be completely completely different, because the animation beneath reveals:

The pale blue states present the states which have been visited over the last iteration. The darkish blue states are the states we attain within the present iteration when reapplying the identical actions.

Visiting completely different states alongside the trail, additionally means accumulating completely different rewards. We’ve got to maintain this in thoughts, particularly since these rewards will later be used within the Backpropagation step to replace the worth estimates. Therefore, now we have to replace the reward member variables of every node alongside the trail.

Allow us to rapidly summarize the stochastic model the choice step: we begin on the root node and select the most effective youngster in keeping with UCT components. Nevertheless, not like within the deterministic case, we don’t simply proceed with the most effective youngster node, however reapply the corresponding motion to root’s state (within the setting). We transit to the subsequent state and acquire a reward. Because of the stochastic nature of the setting each might differ from iteration to iteration. Therefore, we have to replace the reward member variable of the most effective youngster and retailer the newest state. We repeat this course of till we attain a leaf-node.

The repeated updates alongside the most effective path in every iteration in fact require extra computational energy. Moreover, relying on the diploma of stochasticity, extra total iterations could also be wanted to get a enough confidence into the statistics.

Monte Carlo Tree Search — newcomers information
State Values and Coverage Analysis
Relationship between state and motion worth operate in Reinforcement Studying.
Worth Features
Monte Carlo Tree Search
MCTS