It might be excellent if the world of neural community represented a one-to-one relationship: every neuron prompts on one and just one function. In such a world, decoding the mannequin could be simple: this neuron fires for the canine ear function, and that neuron fires for the wheel of automobiles. Sadly, that isn’t the case. In actuality, a mannequin with dimension d usually must symbolize m options, the place d < m. That is once we observe the phenomenon of superposition.
Within the context of machine studying, superposition refers to a selected phenomenon that one neuron in a mannequin represents a number of overlapping options moderately than a single, distinct one. For instance, InceptionV1 accommodates one neuron that responds to cat faces, fronts of automobiles, and cat legs [1]. This results in what we are able to superposition of various options activation in the identical neuron or circuit.
The existence of superposition makes mannequin explainability difficult, particularly in deep studying fashions, the place neurons in hidden layers symbolize complicated mixtures of patterns moderately than being related to easy, direct options.
On this weblog publish, we are going to current a easy toy instance of superposition, with detailed implementations by Python on this pocket book.
We start this part by discussing the time period “function”.
In tabular information, there may be little ambiguity in defining what a function is. For instance, when predicting the standard of wine utilizing a tabular dataset, options could be the share of alcohol, the 12 months of manufacturing, and so on.
Nevertheless, defining options can develop into complicated when coping with non-tabular information, reminiscent of photos or textual information. In these instances, there isn’t a universally agreed-upon definition of a function. Broadly, a function could be thought-about any property of the enter that’s recognizable to most people. As an example, one function in a big language mannequin (LLM) may be whether or not a phrase is in French.
Superposition happens when the variety of options is greater than the mannequin dimensions. We declare that two crucial situations have to be met if superposition would happen:
- Non-linearity: Neural networks usually embody non-linear activation capabilities, reminiscent of sigmoid or ReLU, on the finish of every hidden layer. These activation capabilities give the community prospects to map inputs to outputs in a non-linear manner, in order that it may possibly seize extra complicated relationships between options. We are able to think about that with out non-linearity, the mannequin would behave as a easy linear transformation, the place options stay linearly separable, with none chance of compression of dimensions by means of superposition.
- Function Sparsity: Function sparsity means the truth that solely a small subset of options is non-zero. For instance, in language fashions, many options will not be current on the identical time: e.g. one identical phrase can’t be is_French and is_other_languages. If all options have been dense, we are able to think about an necessary interference as a result of overlapping representations, making it very troublesome for the mannequin to decode options.
Artificial Dataset
Allow us to take into account a toy instance of 40 options with linearly lowering function significance: the primary function has an significance of 1, the final function has an significance of 0.1, and the significance of the remaining options is evenly spaced between these two values.
We then generate an artificial dataset with the next code:
def generate_sythentic_dataset(dim_sample, num_sapmple, sparsity):
"""Generate artificial dataset based on sparsity"""
dataset=[]
for _ in vary(num_sapmple):
x = np.random.uniform(0, 1, n)
masks = np.random.selection([0, 1], dimension=n, p=[sparsity, 1 - sparsity])
x = x * masks # Apply sparsity
dataset.append(x)
return np.array(dataset)
This operate creates an artificial dataset with the given variety of dimensions, which is, 40 in our case. For every dimension, a random worth is generated from a uniform distribution in [0, 1]. The sparsity parameter, various between 0 and 1, controls the share of lively options in every pattern. For instance, when the sparsity is 0.8, it the options in every pattern has 80% probability to be zero. The operate applies a masks matrix to understand the sparsity setting.
Linear and Relu Fashions
We’d now wish to discover how ReLU-based neural fashions result in superposition formation and the way sparsity values would change their behaviors.
We set our experiment within the following manner: we compress the options with 40 dimensions into the 5 dimensional area, then reconstruct the vector by reversing the method. Observing the habits of those transformations, we count on to see how superposition types in every case.
To take action, we take into account two very related fashions:
- Linear Mannequin: A easy linear mannequin with solely 5 coefficients. Recall that we wish to work with 40 options — excess of the mannequin’s dimensions.
- ReLU Mannequin: A mannequin nearly the identical to the linear one, however with an extra ReLU activation operate on the finish, introducing one degree of non-linearity.
Each fashions are constructed utilizing PyTorch. For instance, we construct the ReLU mannequin with the next code:
class ReLUModel(nn.Module):
def __init__(self, n, m):
tremendous().__init__()
self.W = nn.Parameter(torch.randn(m, n) * np.sqrt(1 / n))
self.b = nn.Parameter(torch.zeros(n))def ahead(self, x):
h = torch.relu(torch.matmul(x, self.W.T)) # Add ReLU activation: x (batch, n) * W.T (n, m) -> h (batch, m)
x_reconstructed = torch.relu(torch.matmul(h, self.W) + self.b) # Reconstruction with ReLU
return x_reconstructed
In keeping with the code, the n-dimensional enter vector x is projected right into a lower-dimensional area by multiplying it with an m×n weight matrix. We then reconstruct the unique vector by mapping it again to the unique function area by means of a ReLU transformation, adjusted by a bias vector. The Linear Mannequin is given by the same construction, with the one distinction being that the reconstruction is finished by utilizing solely the linear transformation as an alternative of ReLU. We prepare the mannequin by minimizing the imply squared error between the unique function samples and the reconstructed ones, weighted one the function significance.
We skilled each fashions with completely different sparsity values: 0.1, 0.5, and 0.9, from much less sparse to probably the most sparse. We have now noticed a number of necessary outcomes.
First, regardless of the sparsity degree, ReLU fashions “compress” options significantly better than linear fashions: Whereas linear fashions primarily seize options with the best function significance, ReLU fashions might concentrate on much less necessary options by formation of superposition— the place a single mannequin dimension represents a number of options. Allow us to have a imaginative and prescient of this phenomenon within the following visualizations: for linear fashions, the biases are smallest for the highest 5 options, (in case you don’t keep in mind: the function significance is outlined as a linearly lowering operate primarily based on function order). In distinction, the biases for the ReLU mannequin don’t present this order and are typically decreased extra.
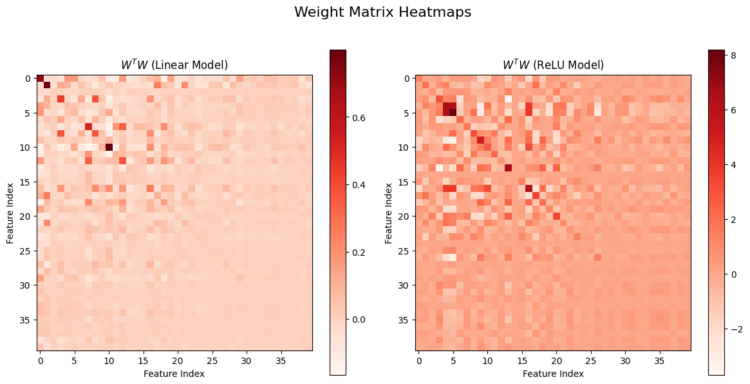
One other necessary and attention-grabbing result’s that: superposition is more likely to look at when sparsity degree is excessive within the options. To get an impression of this phenomenon, we are able to visualize the matrix W^T@W, the place W is the m×n weight matrix within the fashions. One may interpret the matrix W^T@W as a amount of how the enter options are projected onto the decrease dimensional area:
Particularly:
- The diagonal of W^T@W represents the “self-similarity” of every function contained in the low dimensional remodeled area.
- The off-diagonal of the matrix represents how completely different options correlate to one another.
We now visualize the values of W^T@W under for each the Linear and ReLU fashions we’ve constructed earlier than with two completely different sparsity ranges : 0.1 and 0.9. You possibly can see that when the sparsity worth is excessive as 0.9, the off-diagonal components develop into a lot greater in comparison with the case when sparsity is 0.1 (You truly don’t see a lot distinction between the 2 fashions output). This remark signifies that correlations between completely different options are extra simply to be realized when sparsity is excessive.
On this weblog publish, I made a easy experiment to introduce the formation of superposition in neural networks by evaluating Linear and ReLU fashions with fewer dimensions than options to symbolize. We noticed that the non-linearity launched by the ReLU activation, mixed with a sure degree of sparsity, can assist the mannequin kind superposition.
In real-world functions, that are rather more complicated than my navie instance, superposition is a crucial mechanism for representing complicated relationships in neural fashions, particularly in imaginative and prescient fashions or LLMs.
[1] Zoom In: An Introduction to Circuits. https://distill.pub/2020/circuits/zoom-in/
[2] Toy fashions with superposition. https://transformer-circuits.pub/2022/toy_model/index.html